2.1 闭合磁回路磁感应强度计算
传统的永磁式电涡流阻尼器磁感应强度由永磁铁初始的加工所定,部分学者会利用导体板与永磁铁的间距、导体板与背铁板厚度及永磁铁的对数等,来改变涡流阻尼器的阻尼力大小。而EECD利用外部电源的输入,对设备内的磁通量进行了控制,进而改变电涡流阻尼力。在此过程中,由电流产生磁感应强度大小是可以通过计算得出的,计算过程如下:
图3 电磁铁线圈布置图Fig.3 Coil arrangement of electromagnets
如图3所示,先假设BP段仍然布满线圈,先计算出AP段线圈在导体板中心P点产生的磁感应强度B1,再计算BP段线圈在导体板中心P点产生的磁感应强度B2,然后两者相减得出电磁铁映射在导体板上的磁感应强度B。值得说明的是,该计算假设的是磁回路是以铁芯材料为介质,且不存在漏磁情况下。这样的假设更利于我们计算电磁铁在背铁作用下的磁感应强度大小。
AP段磁感应强度:
BP段磁感应强度:
EECD实际线圈中,β→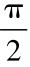 。即:
。即:
结合上述(1)、(2)、(3)式。解得:
由于EECD在实际构造中,L>R≫d,所以该公式该可以简化为:
式(5)中: u=u0ur, u0是真空磁导率,取4π× 10− 7 T∙m/A。ur是材料的相对磁导率。AB段是实际的电磁铁长度,BP段中距离d是电磁铁端口与导体板的间距。L是电磁铁长度,r是线圈的半径, R是电磁铁的半径,n1是电磁铁实际长度对应的匝数,由L + d/2r算出,n是d长度所对应的虚拟匝数由d/2r算出,C是实际线圈捆的层数,u是电磁铁铁芯的磁导率,Z是电磁铁一端圆心到另一端圆外圈斜边长。
由于实际仿真中,导体板与电磁铁存在着一定的气隙,这使得磁回路出现了两种介质干扰的情况,如图4仿真所示,根据多次仿真,及相同工况下同步进行实验测得的结果。我们发现磁感应强度在气隙中的强度大概是铁芯中强度的5%左右,所以在此引入了一种折减系数。最终得出磁感应强度公式:
式(6)中,N为电磁铁的对数,ς为实验及COMSOL Multiphysics多次仿真得出的折减系数,取0.025。
图4 磁场仿真Fig.4 Magnetic field simulation
如图5所示,铜板为导体板,厚度4 mm,A3钢背铁板厚度4 mm,且背铁材料与铁芯一致,空气间隙为4 mm,电磁铁对数为1对时。结合仿真与实测结果显示,在电磁铁铁芯及背铁材料不一样时,其中10号钢相对磁导率为7000,A3钢的相对磁导率为2000,软铁的相对磁导率为700。未施加转动速度情况下,不同大小的电流,不同铁芯的电磁铁在导体板中产生的磁感应强度都不同。利用数显特斯拉计实时检测磁感应强度,数据整合如表1所示,实测结果与仿真结果最大偏差在13.35%,但是理论公式计算整体相对吻合,最大偏差控制在5.03%。这是因为EECD实际构造外侧背铁板与铁芯并非焊接,存在气隙,且材料不同,加上构造存在其他导磁金属,对其磁感应产生了一定的影响。而理论的计算公式考虑了这些因素,所以吻合情况良好。且为了验证线圈不存在铁芯与背铁及存在铁芯与背铁中,磁感应强度区别,以单个线圈、电流2.5 A、 680匝这一工况仿真分析可得,如表2所示,存在铁芯与背铁的磁感应强度相对于通电线圈无铁芯无背铁时的25.24倍,线圈存在铁芯无背铁情况时的4.26倍。
图5 不同电流下磁感应强度Fig.5 Magnetic induction intensity at different currents
2.2 电涡流等效阻尼系数与惯质计算
如图4所示,电磁铁映射在导体板上的磁场分布并不均匀,存在一定的差值,但差距也并不大,所以仍然作匀强磁场来考虑,上述推导中,已经对磁感应强度作出了计算。为了简化计算,仅考虑一块电磁铁在导体板上作用,简化模型如图6所示。假设厚度为t,电阻率为ρ,半径为Rd的导体板外圆正上方放置一个电磁铁。电磁铁产生的磁感应强度为B,导体板以角速度ω水平转动。
表1 A3钢磁感应强度仿真与试验值对比Table 1 Comparison between simulation and experimental values of magnetic induction intensity of A3 steel
表2 电流2.5 A、680匝不同情况下对比Table 2 Comparison under different conditions at current of 2.5 A and 680 turns
图6 阻尼单元的简化模型Fig.6 Simplified model of damping unit
在导体板内取一个位于电磁铁正下方的微导线单元,该单元长度为li,宽度为da,厚度为t。线单元两侧电势差为:
dε=BωRxli(7)
根据图中几何关系,由图6可知:
li =2R sin α(8)
式(7)、(8)中: Rx是导体板中心点到电磁铁正下方中心点的间距,R为电磁铁的半径。
假设电涡流阻尼力达到最大值,则产生的感应电流达到最大,其电阻长度应为2li。
式(9)中: dΩ为导线单元的内电阻, ρ为铜的电阻率,取1.56×10− 8Ω∙m。
单个导线单元通过的电流强度dI为:
单个导线单元受到的安培力:
dF=BlidI(11)
对dF积分可得单个线圈对应的电涡流阻尼力:
从式(12)中,可以看出,当电磁铁与导体板间距一定时,随着转动角速度的增大,其阻尼力也呈线性变化,符合结构动力学中涡流阻尼在低速情况下呈线性变化这一特点。
进而导体板产生的电涡流阻尼系数为:
式(13)中:N为电磁铁的对数。
假设结构基础的运动速度为u̇,通过转动装置相互作用的关系,可以得到导体板与背铁的转动速度。
式(14)中:r1,r2分别为小齿轮和大齿轮的半径。
导体板和背铁为实心圆盘,总转动惯量为:
式(15)中:m,r3分别为导体板和背铁板总的质量和导体板和背铁板的半径,这里导体板与背铁板的半径相同,需要注意的是轴心杆是实心。
最后结合上式可求得惯质为:
式(16)中:i为导体板与背铁板的转速与结构基础的运动速度u̇的比值。
值得一提的是,转速过快时,导体板产生的感应电流会变大,进而会产生与原磁场方向相抵消的磁场,这时的阻尼系数会出现非线性[22]的变化,针对该类问题还有待后续研究。