1.天津城建大学经济与管理学院,天津 300384;2.天津城建大学国际教育学院,天津 300384
1.School of Economics and Management , Tianjin Chengjian University , Tianjin 300384, China;2.School of International Education , Tianjin Chengjian University , Tianjin 300384, China
Earthquake disaster; Emergency shelter; Analytic hierarchy process; Safety evaluation; Disaster prevention and mitigation
DOI: 10.13512/j.hndz.2023.02.12
备注
引言
城市地震避难场所,是地震频发城市用于应对地震灾害及伴生重大突发公共事件的一项灾民安置措施,是能保障灾民震前、震时、震后基本生活而事先划分的带有一定功能设施的场地[1]。通常可将公园、广场、体育场馆等条件适宜的公共场地场所进行一定的完善、改造,使其具备地震应急避难的功能,在平常发挥其原有功能,而在地震灾难发生后作为不同等级的应急避难场所供居民使用。城市地震避难场所的安全与否,直接决定了其在面对地震灾害及伴生重大突发事件时的应急救援能力,也对恢复重建工作有着直接影响[2]。
地震避难场所安全评价,包括场所自身安全性评价与人员生存条件安全性评价两部分内容,是避难场所适宜性的直接体现。国外有关应急避难场所安全评价的相关研究工作开展较早,Ma D等[3]利用层次分析法,采用指标比例尺和多层次灰色评价,提出了一种新的评价村庄地震疏散能力的指标体系。Anhorn J等[4]以加德满都大都市的地震灾害为例,对加德满都大都市内的410个被确定为应急避难场所的开放空间的适宜性进行评价与分类,并在此基础上讨论了该方法的优点和局限性。我国近年来不仅建设了大量的应急避难场所,同时也越来越重视对应急避难场所的安全评价工作。郭晓宇[5]以北京市中关村电子商务中心区为实例,采集了包括道路高宽比、临街建筑玻璃幕墙面积、人行道面积比等在内的43项三级指标,运用德尔菲法和层次分析法计算针对“应急疏散”与“应急救援”功能的各级评价指标权重并进行安全评价,为地震灾时疏散及救援最优路径的选择提供数据参考。熊焰等[6]建立了包含3个层次、18个因素的地震应急避难场所减灾能力评价体系,采用层次分析法对北京市朝阳区的应急避难场所进行评价,验证了提出的地震应急避难场所减灾能力评价体系具有较好的可操作性。史晓瑞[7]基于GIS平台综合运用熵值权重法、灰色关联度分析构建适宜性评价模型,对石家庄市现有9处应急避难场所适宜程度进行评价。马程伟等[8]以昆明市东川区地震应急避难场所为研究对象,结合Arc GIS软件从可达性、服务面积比和空间基尼系数三个指标评价应急避难场所空间布局的合理性。王进等[9]以云南省嵩明县主城区已建的9处地震应急避难场所为例,以场所的有效性、可达性以及安全性为对象构建评价适宜性指标体系,采用灰色关联分析结合熵值权重法对其进行适宜性评价并划分适宜性等级。杜亚男[10]利用“地震应急避难场所+”模式,将宁夏海原县老城区的应急避难场所与公园绿地、学校、公共大型建筑等结合,提出从前期受灾人口预测到避难场所选取再到对应急避难场所评价一体化规划方法。同时,采用公共区位理论对地震应急避难场所进行规划,在建筑易损性分析、受灾人口预测、构建应急避难场所评价指标体系和方法的基础上,对应急避难场所进行评价和优化。苏建锋等[11]利用熵值权重与灰色关联分析相结合的评价模型和GIS空间分析方法,以构建的应急避难场所适宜性评价指标体系为研究基础,对天津市中心城区地震应急避难场所进行适宜性评价,研究成果对增强城市应急避难场所规划、建设合理性及提高应急处理能力具有一定指导意义。
我国地震应急避难场所还存在“重建设、轻管理”的问题[12],存在场所建设不达标、设备设施配备不齐全、管理措施不完善、宣传引导不到位等问题。公园是城市快速发展的重要名片,也是丰富人民精神生活、串联城市各项功能的关键载体。城市公园多位于人员居住密集的区域,具有面积大、通达性好、基础设施较为完备等特点,适宜作为自然灾害或突发事件的应急避难场所,在城市安全稳定发展中也起到了举足轻重的作用。本文即从城市地震应急避难场所的安全性角度出发,以某公园类型的应急避难场所为例,基于层次分析法等理论开展地震应急避难场所安全评价研究,探讨公园类型的应急避难场所在城市避难中的可行性与安全强化方向。
-
1 地震应急避难场所安全评价方法
1.1 层次分析法层次分析法是指将决策问题的有关因素分解成目标、准则、方案等层次,用一定标度对人的主观判断进行客观量化,在此基础上进行定性分析和定量分析的一种决策方法[13-14]。该方法建立在专家经验判断的基础上,按因素间相互关联影响以及隶属关系将多源因素划分为不同层次,并比较两两因素间相对重要性,再通过定性分析、定量计算获得最优解以提高评价结果的准确性,其计算步骤如下[15-16]:
(1)构造层次分析结构。一般将决策的目标、考虑因素、决策对象按照之间的相互关系分为最高层、中间层、最底层,并绘出结构层次图。最高层为目标层;中间层为准则层,即为一级指标层;最底层为方案层,也就是二级指标层。
(2)构造判断矩阵。将准则层中每个准则下的各方案进行两两对比,按其重要性程度评定等级。假设子系统AK(K=1,2,…, m)的总权重为ak,指标Bi相对于子系统AK的单权重为bi。其中,Ak关联的指标由m个,记为,B1,B2,…,Bm;其单权重记为,b1,b2,…,bm。通过专家评议,确定Bi指标相对于Bj指标的相对重要性的比值bij,其表示要素i与要素j的重要性比较结果,确定除bij和bji的值后,就能构成一个两两相比较的判断矩阵,矩阵中取值要求[15]。
(3)层次单排序与一致性检验。利用方根法按如下公式计算最大特征根λmax及相应的标准化特征向量W,W的元素为同一层次因素对于上一层次某因素相对重要性的排序权值,这一过程称为层次单排序。计算判断矩阵每一行元素的乘积Mi:

计算Mi的m次方根
 对向量
对向量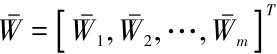 正规化处理,可获得特征向量:
正规化处理,可获得特征向量:

计算判断矩阵的最大特征根:

其中,( AW )i表示向量AW的第i个元素。
在完成层次单排序后,需要对判断矩阵进行一致性检验,确保判断矩阵在逻辑上的合理性,保证后续层次分析具有实际意义。
①确定一致性指标CI:

②确定平均随机一致性指标RI,随机一致性指标RI的取值与判断矩阵的阶数对应关系如表1所示。
③计算一致性比例CR:

表1 平均随机一致性指标标准值Table 1 Standard value of average random consistency index
当CR<0.1时,则该判断矩形通过一致性检验,各元素之间的重要性关系合理,层次单排序的结构有满意的一致性;若CR>0.1 时,则认为不具有一致性,说明专家讨论协商构造的判断矩阵误差较大,需要重新构建判断矩阵,调整判断矩阵的元素取值。
(4)层次总排序与一致性检验。第n-1层h个元素相对于目标层的权重为:
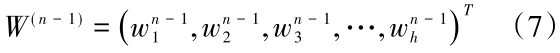
第n层k个元素对于上一层(第n-1层)第j个元素的单排序权重为:
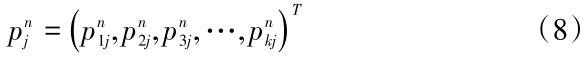
其中与j无关的元素的权重为0,令:
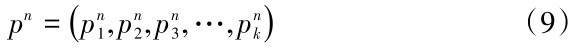
表示第n层元素对下层元素的排序,则第n层元素的总排序为:
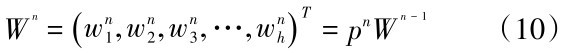
总排序一致性检验与单排序一致性检验步骤类似:
计算总一致性指标CI:
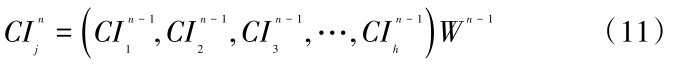
确定平均随机一致性指标RI:
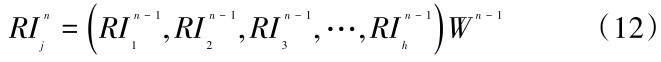
计算总一致性比例:

当CR n<0.1时,该判断矩形通过一致性检验。(5)分析排序结果,得出最优方案。
1.2 德尔菲法德尔菲法,是将专家作为索取信息的对象,以专家的经验、知识为依托,对问题做出判断、评估和预测的一种方法[17]。德尔菲法在本质上是一种反馈匿名函询法,在预测问题得到专家的答复后,进行相应的归纳、统计,将结果匿名反馈给每个专家,征求专家的答案,再归纳统计并进行反馈,直至专家意见基本保持一致[18]。由于专家们处于互不知情的隔离状态,每个人的信息是自己的知识、经验、专长以及调查机构反馈给他们汇总情况的集中体现,便于集中智慧。德尔菲法与一般的判断预测方法相比,可以充分利用专家的经验和知识,保证最终的结论的准确性和有效性[19]。
1.3 综合指数法综合指数法的主要用途是将各项指标转化为同一测度的单项指标,便于将各项指标进行综合,并以综合指标作为综合价值排序的依据。指标权重根据其重要性确定,反映指标在综合价值中的作用[20]。利用1.1节与1.2节中介绍的层次分析法计算的权重和德尔菲法取得的数值进行累乘,然后将各项的得分数值相加,最后可计算出综合评价指数[21]。评价公式如下:

式(1 4)中: M为评价得分; Ki为一级指标权重系数;Kij为二级指标权重系数;Mij为指标分值;i为一级指标数;j为二级指标数;n为一级指标个数, m为某一级指标包含的二级指标个数。
1.4 安全评价流程基于层次分析法、德尔菲法和综合指数法原理,所研究的地震应急避难场所的安全评价流程如下:
(1)针对所研究的地震应急避难场所,开展包括周边交通、出入口、疏散通道、防灾配套设施等方面的安全性调研工作,为地震应急避难场所安全性评价提供基础依据;
(2)归纳总结出影响城市地震应急避难场所安全性的主要因素,建立多层次、多指标的地震应急避难场所安全评价指标体系,根据现行规范、标准等确定各指标的安全评价标准;
(3)根据(2)中确定的指标体系,利用层次分析法针对一级指标与二级指标,建立相应的判断矩并计算各指标对应的权重值,验证其一致性;
(4)采用德尔菲法,邀请行业内一定数量的专家,根据公园的具体调研情况、基本特征的了解和判断,对各研究避难场所内各二级指标的完成度与适宜性进行打分,取各指标平均值作为安全评价分数;
(5)最后利用综合指数法,利用公式(14)计算各二级指标在各自权重值下的得分,累积相加和得到综合评价的最终得分,以实现地震应急避难场所的安全评价。
-
2 地震应急避难场所安全性调研
2.1 基本情况某公园地震应急避难场所的周边有三条以上主干道路,道路安全畅通、交通十分便利。公园周围无铁路、高压输变电线路、易燃易爆物或核放射物储放地和60 m以上的建(构)筑物。公园地势较高,地质状况良好,地下无断层分布,远离洪涝、地质灾害等水文地质条件恶劣区域和其它自然灾害易发生地段。该地震应急避难场所始建于2008年初,2010年底全部完成,是所在地区的首个符合国家标准的地震应急避难场所。公园占地面积32.4万m2,绿地面积22万m2,可容纳人数7万人,紧急情况下可容纳10万人临时避难。同时具备综合设施配置,可安置受助人员30天以上,属于Ⅰ类地震应急避难场所。
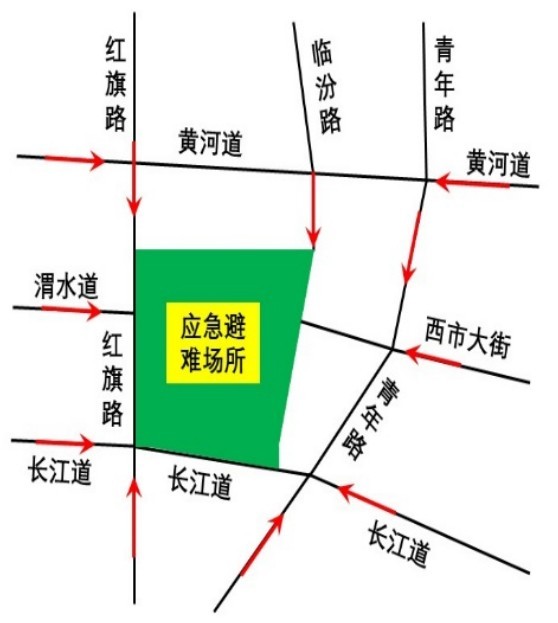
2.2 规划布局2.2.1 公园出入口根据周边道路情况和通达性的要求,公园在东南西北四个方向都设有入口,其中东、西两面共设两个主入口,宽度均在15 m以上。西面入口紧邻主干道,东面入口附近有商业写字楼,发生地震灾害时主要疏散办公楼的工作人员和小区居民。入口采用可移动式围挡,地震灾害时可以很快撤去,保证了可通达性。除主入口外另设有五个次入口,入口宽度至少在5m以上,其中:西面3个,包括一个人行入口,一个用于车辆进入的入口,一个用于自行车进入的入口;北面入口与临近的居住小区相连,主要用于灾时住区居民的疏散;南面入口为临时型入口,仅能单人通行,不能作为地震应急避难时的疏散入口使用。
2.2.2 地震应急疏散通道公园外侧有东南西北四个不同方向的多条与外界相通的地震应急疏散道路(如图1中红色实线所示),方便人们在地震灾难发生后就近选择地震应急避难场所进行紧急避难。
-
3 地震应急避难场所安全评价
本文以某公园应急避难场所为例,结合公园类型的地震应急避难场所特点,构建地震应急避难场所安全评价模型,开展城市地震应急避难场所的安全评价研究。
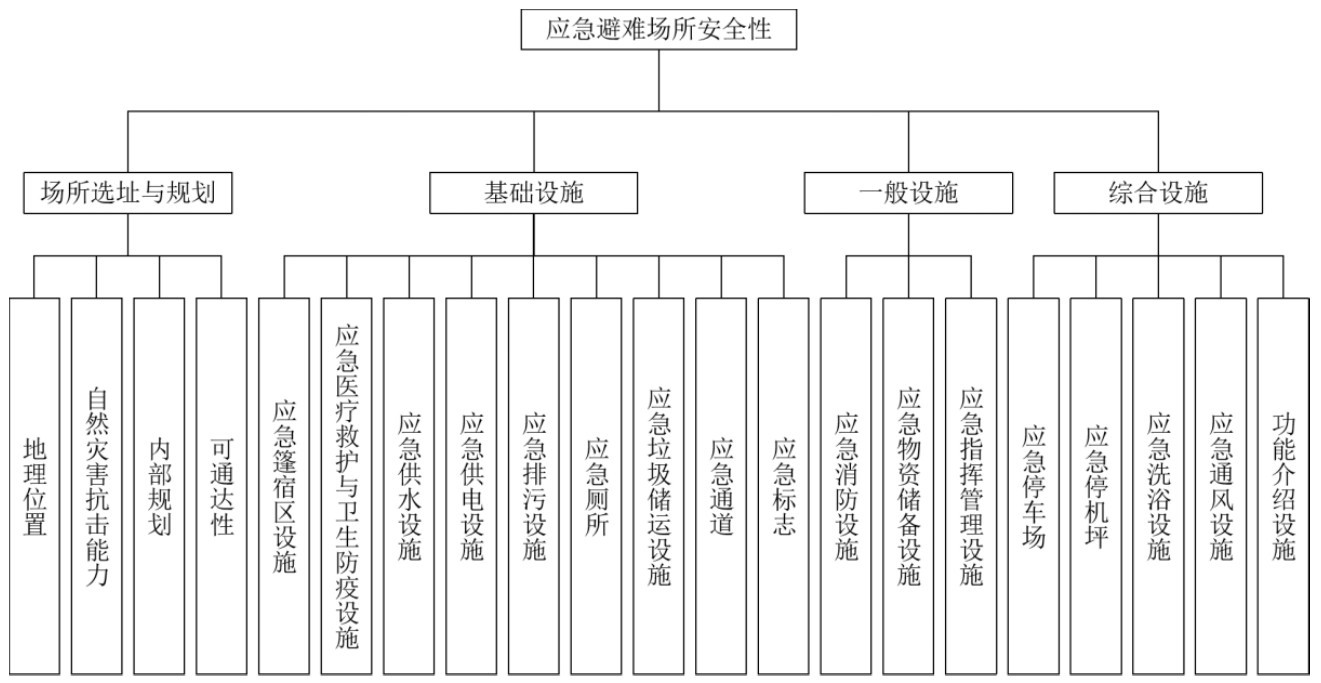
3.1 安全评价指标以城市地震应急避难场所的安全性作为研究目标,结合某公园地震应急避难场所的调研情况与国家应急避难场所建设标准[22-23],归纳出对城市地震应急避难场所安全性影响性最大的因素主要包括场地的选址与规划和场地的设施配备,其中场地的设施配备由于作用不同又分为基础设施、一般设施和综合设施。结合层次分析法的分析原理,可以将场所选址与规划、基础设施、一般设施、综合设施设置为准则层,即一级指标。再根据城市地震应急避难场所的相关建设标准,将准则层中包含的具体方案进行总结,故在方案层共可以整理出21个二级评价指标。评价指标结构层次如图2所示。
图2 评级指标层次结构图Fig.2 Hierarchy chart of rating indicators
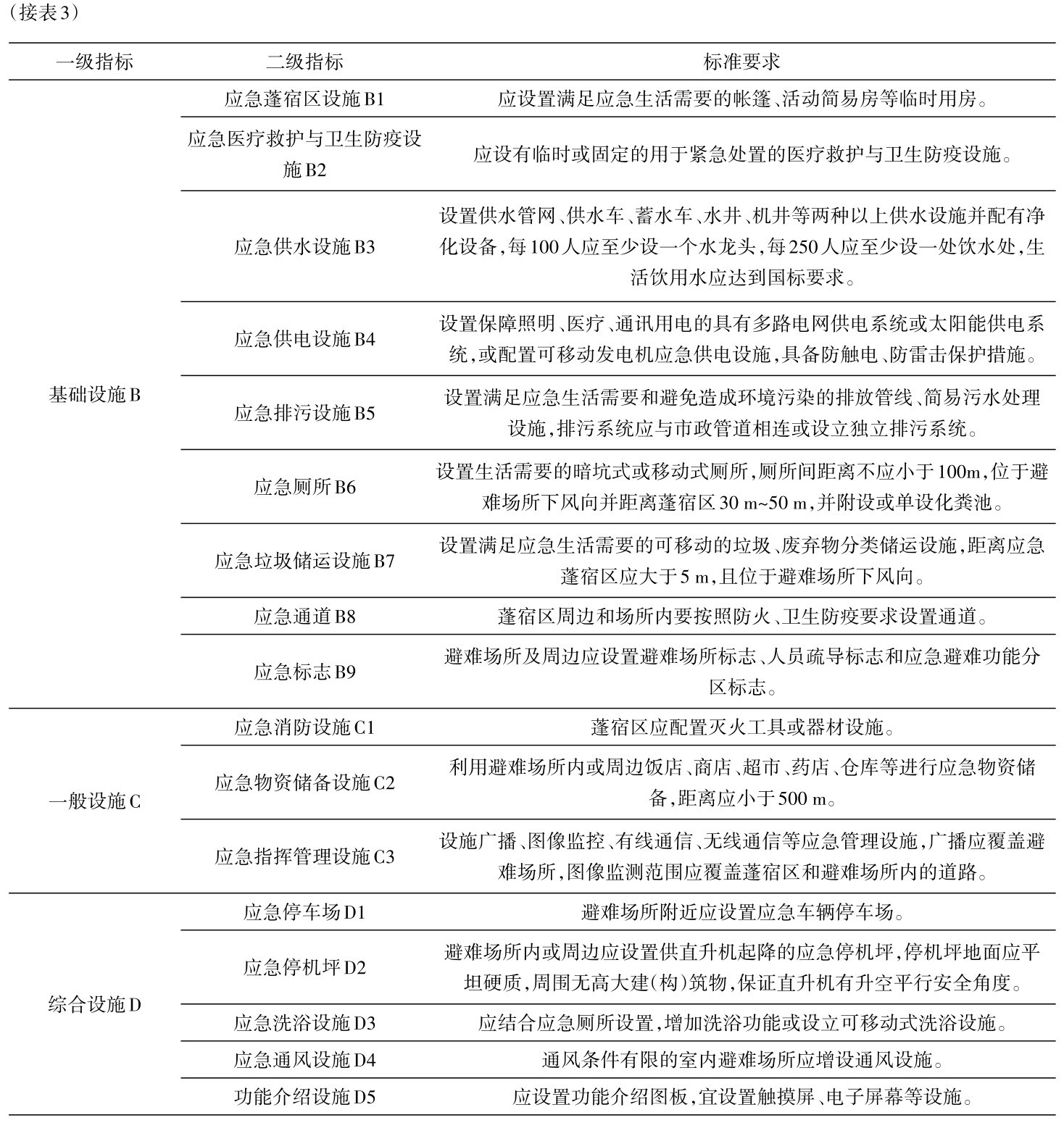
3.2 安全指标的评价标准在确定安全指标后,再根据国家应急避难场所建设标准[22-23],为准则层的一级指标与方案层的二级指标提供确定各自评价标准的参照,具体评价标准与要求如表3所示。
表3 应急避难场所安全评价标准表Table 3 Safety evaluation criteria of emergency shelters
 3.3 安全指标权重3.3.1 一级指标
3.3 安全指标权重3.3.1 一级指标根据上述指标体系,邀请行业专家进行协商讨论,建立准则层一级指标的判断矩阵如表4所列,根据公式(1)~(4)可以计算判断矩阵S的最大特征根为λmax=4.0104。
为检验判断矩阵的一致性,根据公式(5)计算一致性指标CI:
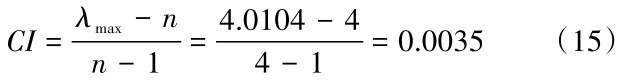
表4 一级指标判断矩阵Table 4 Judgment matrix of primary index
由一级指标判断矩阵为4阶,根据表2可确定平均随机一致性指标RI=0 . 9 ,根据公式(6)可以计算随机一致性比例CR:

因此该层次分析结果通过一致性检验,认为该权系数的分配是合理的,近一步说明专家构造的判断矩阵误差合理,不需要调整。根据公式(1)~(3)可以计算一级指标的权重值分别为 0.3509、0.3509、0.1891、0.1091。
3.3.2 二级指标针对安全指标体系中准则层内每个一级指标,即“场所选址与规划”、“基础设施”、“一般设施”、“综合设施”,分别对其内部的二级指标进行两两比较,可构造4个判别矩阵S=( uij )p×p ,指标间相互比较结果见表5~表8所列。
表5 场所选址与规划判断矩阵Table 5 Judgment matrix of site selection and planning
表6 基础设施判断矩阵Table 6 Judgment matrix of infrastructure
表7 一般设施判断矩阵Table 7 Judgment matrix of general facilities
表8 综合设施判断矩阵Table 8 Judgment matrix of comprehensive facilities
再利用层次分析法,计算获得各准则层指标判断矩阵S的最大特征根、检验判断矩阵的一致性的指标与随机一致性比例见表9所列。
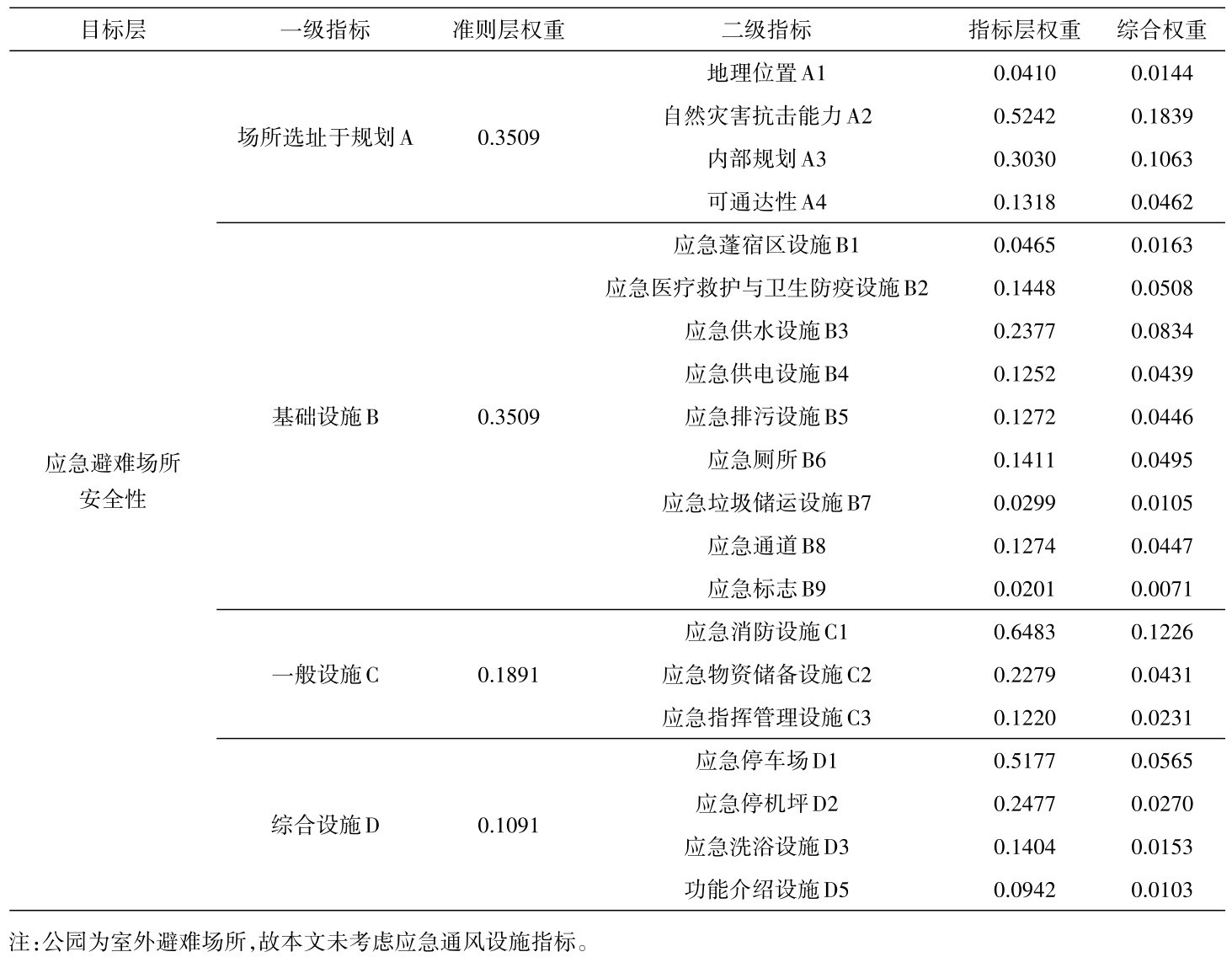
由表9可知,各准则层层次分析结果均通过一致性检验,认为各准则权系数的分配是合理的。因此,根据公式(1)~(3)可以计算各准则层指标“场所选址与规划”、“基础设施”、“一般设施”、“综合设施”的二级指标权重值与综合权重值见表 10所列。
3.4 安全评价运用德尔菲法,邀请本专业的10名专家,参考该公园的设施配备情况调研结果(表2所列)与国家应急避难场所安全评价标准(表3所列),结合专家自身经验与对公园应急避难条件的判断,对该公园的各项安全指标按照表 11安全性评价等级进行了打分,具体得分见表 12所示。
表9 各准则层计算参数Table 9 Calculation parameters of each criterion layer
表 10 权重计算结果Table 10 Weight calculation results
表 11 应急避难场所安全性评价等级表Table 11 Safety evaluation grade of emergency shelter
表 12 某公园地震应急避难场所安全指标得分表Table 12 Safety index score of earthquake emergency shelter in one park
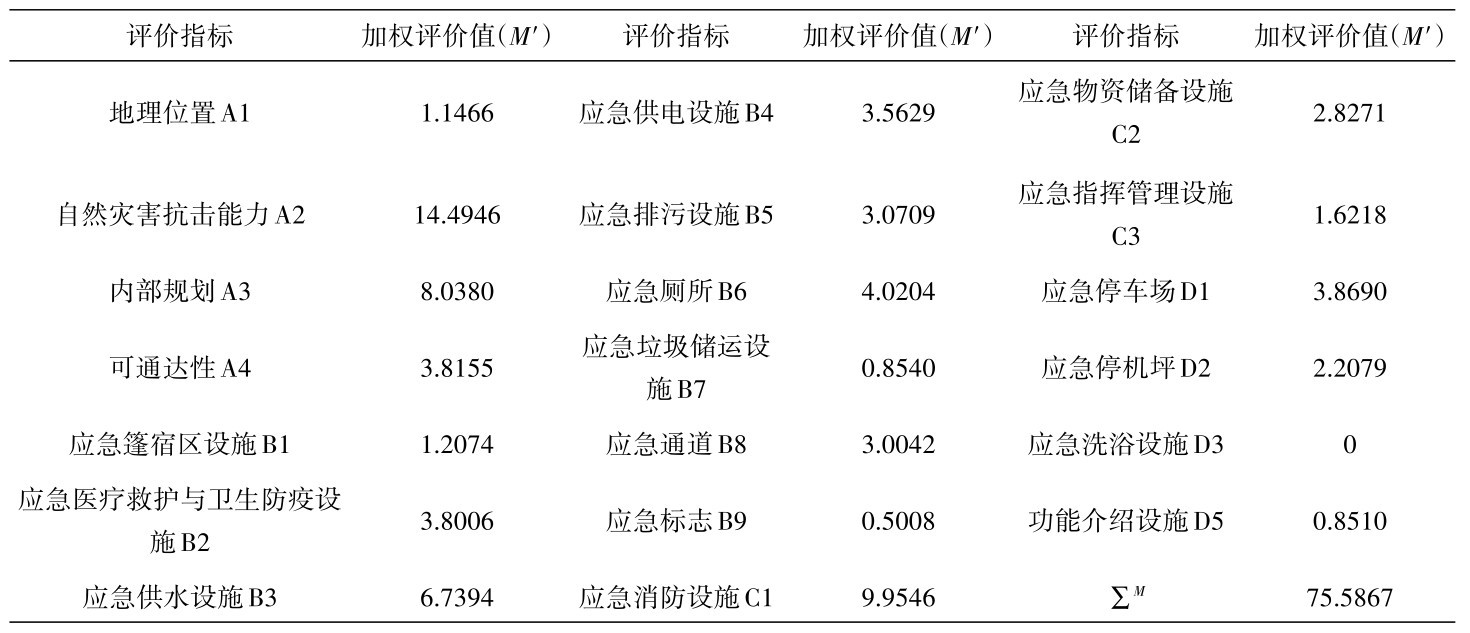
根据1.3节介绍的综合指数法的评价方法,构建安全评价模型。并根据公式(14),将每个二级安全评价指标的权重和其所属一级指标权重相乘得到每个指标的实际权重,再乘以地震应急避难场所该项评价指标的指标得分,得到该项指标加权分值,将每项二级指标的分值相加得到最终的安全评价得分。将前文计算出的表 10所列的一级指标、二级指标的权重值以及表 12中的各项指标的安全评价值,代入公式计算得到某公园地震应急避难场所的安全评价值见表 13所示。
表 13 某公园地震应急避难场所安全评价值Table 13 Safety evaluation value of earthquake emergency shelter in one park
由计算结果可知,影响所研究地震应急避难场所安全性的“可通达性”、“应急供水设施”、“应急供电设施”等8项指标的安全得分超过80,最高得分为“功能介绍设施”指标的82.8,说明上述指标非常满足安全要求,可以继续保持。安全指标得分在70~80之间的,包括“地理位置”、“自然灾害抗击能力”、“内部规划”等7项指标,最高得分为“地理位置”指标的79.7,最低得分为“指挥管理设施”指标的70.3,说明上述指标工作状态良好,但是对于上述指标在应急避难场所中的落实情况还需要适当加强。而包括“应急排污设施”、“应急通道”、“物资储备设施”等5项指标安全得分低于70,体现目前地震应急避难场所中这些指标的达成情况较为一般,特别是“应急洗浴设施”指标还没有落实,需要重点加强与改善。将上述计算结果加和可知,某公园地震应急避难场所的安全评价得分为75.5867分,根据表 11地震应急避难场所安全性评价等级表中的评价等级,某公园地震应急避难场所的安全性属于B等级,工作状态属于“良好”状态,但在部分安全性指标上应该“适当加强”。
-
4 结论
本文着眼于城市地震应急避难场所的安全性评价,利用综合应用层次分析法、德尔菲法、综合指标法构建了考虑公园类型的地震应急避难场所的安全评价体系,并对某公园地震应急避难场所的实际情况进行安全性评价,获得如下主要结论。
(1)基于综合应用层次分析法、德尔菲法、综合指标法构建了城市地震应急避难场所的安全评价方法体系,根据现场调研情况建立了地震应急避难场所安全评价体系,以某公园为研究对象验证了评价方法的可操作性。
(2)对某公园类型地震应急场所开展安全评价研究,结论是其安全性属于B等级,工作状态属于“良好”状态。
(3)根据地震应急避难场所安全评价值计算结果,“急排污设施”、“应急通道”、“物资储备设施”、“应急停车场”、“应急洗浴设施”这5项指标安全得分偏低,特别是“应急洗浴设施”指标在该地震避难场所内尚未落实,使得避难场所的安全性上还应当从上述指标方向进行重点加强,以提高该公园地震应急避难场所的安全性。
- [1]钱洪伟.城市应急避难场所规划环境评价理论及应用研究探析[J].中国公共安全(学术版),2010,5(2):59-63.
- [2]黄典剑,吴宗之,蔡嗣经,等.城市应急避难所的应急适应能力——基于层次分析法的评价方法[J].自然灾害学报, 2006,15(01):52-58.
- [3] Ma D,Chu J. Study on evaluation of earthquake evacuation capacity in village based on multi-level grey evaluation[J]. Systems Engineering Procedia,2011(1):85-92.
- [4] Anhorn J,Khazai B. Open space suitability analysis for emergency shelter after an earthquake[J]. Natural Hazards&Earth System Sciences,2015,2(6):789-803.
- [5]郭晓宇.城市中心区地震应急通道安全评价方法研究及应用[D].北京:北京工业大学,2014.
- [6]熊焰,梁芳,乔永军,等.北京市地震应急避难场所减灾能力评价体系的研究[J].震灾防御技术,2014,9(04):921-931.
- [7]史晓瑞.石家庄市应急避难场所适宜性评价[J].震灾防御技术,2016,11(3):656-666.
- [8]马程伟,方硕,储帅.山地小城市地震应急避难场所布局合理性评价研究——以昆明市东川区为例[J].价值工程, 2018,37(13):23-26.
- [9]王进,吴亮,郭亚容,等.嵩明主城区地震灾害应急避难场所适宜性评价[J].西南林业大学学报(社会科学),2020,4 (05):73-80.
- [10]杜亚男. “地震应急避难场所+”避难新模式研究——以宁夏海原县老城区为例D].银川:宁夏大学,2021.
- [11]苏建锋,张庆斌.城市地震应急避难场所适宜性评价——以天津市中心城区为例[J].震灾防御技术,2021,16 (02):414-420.
- [12]陈江驰,刘仲达,丁俊芳.地震应急避难场所建设存在的问题及建议[J].中国应急救援,2012,04:25-27.
- [13]王莲芬,许树柏.层次分析法引论[M].北京:中国人民大学出版社,1990.
- [14] Saaty T L. The analytic hierarchy process[M]. New York:McGraw Hill International,1980.
- [15]杜栋,庞庆华,吴炎.现代综合评价方法与案例精选(第3版)[M].北京:清华大学出版社,2015.
- [16]刘云忠,郝原.统计综合评价方法与应用[M].北京:清华大学出版社,2020.
- [17]余波.现代信息分析与预测[M].北京:北京理工大学出版社,2011:58-59.
- [18]王光辉,肖圣才,刘小燕,等. Delphi专家评分法在景观桥梁方案比选中的应用[J].湖南理工学院学报(自然科学版),2011,23(3):79-82.
- [19]卢银娟,王颖.科技情报研究专家咨询评价方法[C]//中国科学技术情报学会.情报研究与竞争情报学术研讨会.北京:中国科学技术出版社,2006:91-95.
- [20]梁前德.基础统计[M].北京:高等教育出版社,2011:193-194.
- [21]孙成勋,李红彦,李润琴,等.层次分析法在管理水平综合评价中的应用[J].工业技术经济,2013,30(9):72-78.
- [22]中国标准化委员会.地震应急避难场所场址及配套设施:GB 21734-2008[S].北京:中国质检出版社,2008.
- [23]中华人民共和国住房和城乡建设部.防灾避难场所设计规范:GB51143-2015(2021年版)[S].北京:中国建筑工业出版社,2022.