基金项目:亚热带建筑科学国家重点实验项目(2017KB13)
作者简介:廖宁(1995- ),男,硕士研究生,主要从事结构振动与控制研究。
通信作者:陈太聪(1977- ),男,博士,副教授,主要从事结构振动与控制研究。E-mail:cvchentc@scut.edu.cn
(1. 华南理工大学 土木与交通学院,广州 510640;2. 亚热带建筑科学国家重点实验室,广州 510640)
(1. South China University of Technology,School of Civil Engineering and Transportation,Guangzhou 510640,China;2. State Key Laboratory of Subtropical Building Science,Guangzhou 510640,China)
Viscoelastic damper;Fractional derivative;Riemann-Liouville integral;Caputo derivative;Predictor-corrector method
DOI: 10.13512/j.hndz.2021.02.15
分数阶导数模型可以全面地反映粘弹性阻尼器的力学性能和变化机制,但其中的Riemann-Liouville积分复杂,给减震结构的动力响应求解带来一定的困难。传统分析方法仅考虑结构基频的影响,通过等效刚度和等效阻尼简化结构响应计算,计算结果精度有限。针对含分数阶导数粘弹性阻尼器的减震结构,通过引入Caputo分数阶导数及相关高阶预估-校正技术,提出一种高精度的动力响应直接数值解法。通过多层结构算例,检验本文算法的有效性,对比考察了传统等效方法在不同简谐激励及El Centro地震波作用下的相关计算偏差。
The fractional derivative model can fully represent the mechanical properties and the changing mechanism of viscoelastic dampers,however,the Riemann-Liouville integral involved is complex,which brings difficulties to the solution of dynamic structural responses. The conventional method often takes the fundamental natural frequency of the structure into account to obtain the equivalent stiffness and damping provided by the damper,which can simplify the solution while provides results with limited accuracy. In this paper,a high-precision numerical method to directly solve dynamic responses is proposed by introducing the Caputo fractional derivative and a corresponding high-order predictor-corrector algorithm. The effectiveness of the proposed method is verified via a numerical example of a multi-story structure,and comparisons with the conventional equivalent method are carried out to identify the relative errors of dynamic responses under different harmonic excitations and the EI Centro seismic wave.
粘弹性阻尼器作为一种被动耗能装置,目前广泛应用于耗能减震工程中[1-2]。众多学者经过大量实验研究发现[3-5],温度、频率、应变幅值和加载循环次数是影响粘弹性材料力学性能的主要因素。在实际地震工程中,由于地震激励的持时短暂,阻尼器的温度变化不大,地震峰值加速度的出现次数较少,因此,温度、应变幅值与加载循环次数对阻尼器的影响不显著,频率成为粘弹性阻尼器在实际地震工程应用中主要考虑的影响因素[3]。
在粘弹性阻尼器的众多本构模型中,分数阶导数模型可以较为精确合理地描述阻尼器的力学性能,但其中的Riemann-Liouville积分复杂,给减震结构的动力响应求解带来一定的困难。在实际工程应用中,通常只根据结构基频,近似粘弹性阻尼器的等效刚度与等效阻尼,进而简化求解结构动力响应[6-7]。然而结构存在多阶自振频率,传统方法忽略了结构高阶自振频率对阻尼器带来的影响,导致速度和加速度等高阶效应较大的响应精度较低。与此同时,粘弹性阻尼器的加入会改变结构的刚度分布及相应自振频率,只采用结构原始基频计算粘弹性阻尼器的参数也可能导致一定误差。另一方面,在实际地震中,地震激励存在多个激励主频,当结构基频与地震激励主频相差较大时,也可能造成计算结果与实际结果有较大出入。
本文基于分数阶导数模型,建立含粘弹性阻尼器的减震结构的运动方程,通过引入Caputo分数阶导数及相关高阶预估-校正计算技术,提出一种高精度的动力时程响应直接数值解法。通过多层结构算例,检验本文算法的有效性,考察传统等效方法在不同简谐激励及EI Centro地震波作用下的相关计算偏差。
在众多的粘弹性阻尼器本构模型中[8-11],分数阶导数模型[11]能较好地描述频率、应变幅值对粘弹性阻尼器性能的影响规律,并采用温频等效原则反映了温度所带来的影响,应用起来较为精确合理。分数阶导数的应力-应变关系表示如下[6]:
τ(t)+aDδτ(t)=G[γ(t)+bDδγ(t)] (1)
式(1)中,τ(t)和γ(t)分别为粘弹性材料的剪应力和剪应变;G为材料弹性参数;Dδ=dδ/dtδ为分数导数算子;δ为分数导数的阶次,0<δ<1;a、b为温频等效参数,a=aref/cδ,b=bref∕cδ;aref、bref为在参考温度Tref下的参数a、b值;c=Tθ/Tθref为温频转换系数;T为温度;θ为粘弹性阻尼器常数。
Dδτ(t)和Dδγ(t)采用Riemann-Liouville积分分别定义如下:
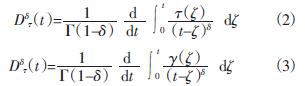
在简谐激励作用下,以上公式经过复频域变换及相关推导,可得到阻尼器的储能剪切模量G'和损耗剪切模量G''分别为[12]:

式(4)、(5)中,ω为激励频率。
根据粘弹性阻尼器性能的频率相关性,在频率为ω的简谐荷载作用下,Soong提出以等效刚度和等效阻尼计算阻尼器的恢复力[6]:
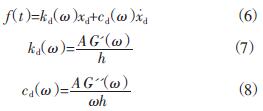
式(6)、(7)中,f为粘弹性阻尼器提供的阻尼力;xd、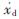 分别为阻尼器两端的相对位移与相对速度;kd(ω)、cd(ω)分别为阻尼器的等效刚度与等效阻尼;A、h分别为粘弹性阻尼器的有效面积与厚度。
分别为阻尼器两端的相对位移与相对速度;kd(ω)、cd(ω)分别为阻尼器的等效刚度与等效阻尼;A、h分别为粘弹性阻尼器的有效面积与厚度。
在一般动力荷载作用下,传统算法考虑结构基频响应的主要影响,根据结构基频计算粘弹性阻尼器的等效刚度与等效阻尼,再由更新后的结构运动方程,求解减震结构的动力响应[7]。该法简单方便,易于工程实现,但计算结果存在一定的近似性。要获得高精度的计算结果,仍需要从包含粘弹性阻尼器本构模型的减震结构完备运动方程出发,探讨基本方程的直接数值求解方法。
一般性,包含层间粘弹性阻尼器的多层减震结构模型如图1所示。在地震激励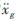 (t)作用下,其运动方程为:
(t)作用下,其运动方程为:
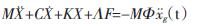 (9)
(9)
式中,
X=[x1 x2 … xn]T (10)
F=[f1 f2 … fn]T (11)
其中,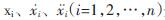 分别为第i层结构的位移、速度与加速度;mi 、ki分别为第i层结构的质量、刚度系数;C为结构的阻尼矩阵;fi为第i层粘弹性阻尼器的恢复力;Λ与Φ分别为阻尼器恢复力与外激励的定位矩阵。
分别为第i层结构的位移、速度与加速度;mi 、ki分别为第i层结构的质量、刚度系数;C为结构的阻尼矩阵;fi为第i层粘弹性阻尼器的恢复力;Λ与Φ分别为阻尼器恢复力与外激励的定位矩阵。
根据式(1)定义的应力-应变关系,可建立第i层粘弹性阻尼器的恢复力与各层位移的关系为[12]:
fi(t)+aDδfi(t)=k'[xi(t)-xi-1(t)]+k'bDδ[xi(t)-xi-1(t)] (12)
式中,k'=GA/h。
由前述可知,要获得减震结构的动力响应,需要联立式(9)与式(12)进行求解。其中,为了方便进行两组方程间的迭代计算,本文将式(12)改写为:
fi(t)=-aDδfi(t)+k'[xi(t)-xi-1(t)]+k'bDδ[xi(t)-xi-1(t)] (13)
由式(2)和(3)所示的分数阶导数定义可见,式(13)中包含有两项Riemann-Liouville积分,不易计算,因此给减震结构的动力响应计算造成了较大困难。
在数学分析中,与时间相关的分数阶导数除了Riemann-Liouville定义,还可采用Caputo定义。后者可以选择和整数阶导数问题相同的初始条件[13],为相关动力方程的求解提供了极大的便利。当满足条件0<δ<1时,Riemann-Liouville分数阶导数与Caputo分数阶导数间存在以下转换关系[14]:
 (14)
(14)
式中,RLsDtδ f为Riemann-Liouville分数阶导数算子;CsDtδ为Caputo分数阶导数算子;Γ( )为伽马函数;t与s分别为积分上、下限,且满足s<t,本文中s=0。
关于Caputo分数阶导数的数值求解,有多种方法可使用[15]。其中,本文为了提高迭代效率,采用一种高阶预估-校正算法,Adams-Moulton法[16],对式(14)中Caputo分数阶导数进行求解。该方法是一种隐式多步线性法,可视为传统隐式方法与预估校正技术的结合,既保留了隐式方法的强稳定性和精确性,又具有预估-校正技术易于实现的特点,有效弥补了各自的不足。其相关计算公式为:
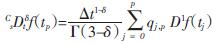 (15)
(15)
式中,Δt为离散时间步长;p=[0,1,2…N],N为全计算时长的总离散步数;qj,p取值如下:
当j=0时,
qj,p=(p-1)2-δ-p1-δ(p+δ-2)
当0<j<p时,
qj,p=(p-j-1)2-δ-2(p-j)2-δ+(p-j+1)2-δ
当j=p时,
qj,p=1
式(15)中的D1f(tj)为阻尼力的一阶导数,可以由[f(tj)-f(tj-1)]/Δt近似计算。
需要说明的是,式(13)中的Dδ[xi(t)-xi-1(t)]也采用与式(15)一致的计算公式进行求解,但其中的相对位移的一阶导数精确等于相对速度,无需进行一阶差分近似。
在对减震结构的动力响应进行逐时刻求解时,在在每一时刻均需结合式(13)~(15),根据假设位移和速度,计算阻尼器恢复力,继而代入方程式(9),更新求解位移和速度响应,再回代入式(13)~(15),更新求解阻尼器恢复力;如此往复迭代,待本时刻的阻尼器恢复力、结构位移和速度响应迭代收敛后,即可进入下一时刻的计算。
为检验本文算法的有效性,取图1所示的10层钢框架结构进行数值分析。结构各层的层质量和层间刚度分别取为mi=8×105 kg和ki=2×108 N/m(i=1,2,…,10)。结构阻尼矩阵取为C=0.0785 M+0.0029 K。各层安装的粘弹性阻尼器均相同,面积A=0.0976 m2,厚度h=0.0635 m,弹性参数G=2.5×106。在外荷载作用的短时间内,可认为粘弹性阻尼器处于恒温工作状态,a、b分别取为0.0347和4.16,分数导数阶次δ=0.71[17]。
通过模态分析,已知结构在未加粘弹性阻尼器之前的各阶自振频率分别为2.3632 rad/s、7.0367 rad/s、11.5531 rad/s、15.8114 rad/s、19.7165 rad/s、23.1811 rad/s、26.1280 rad/s、28.4911 rad/s、30.2179 rad/s、31.2696 rad/s。
为研究在不同频率的简谐激励下,传统等效算法与本文算法的差别,分别输入2组不同频率的简谐地面加速度激励:
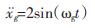 (16)
(16)
其中,ωg分别取为2.5 rad/s与15 rad/s。激励时长取为30 s,离散时间步长为0.02 s。
由于本文方法采用Adams-Moulton技术进行分数阶导数的近似计算,因此,本文方法的计算精度与离散时间步长有关,表中分别采用0.02 s和0.01 s两种时间步长进行计算,以此评估求解精度。
在两组不同的简谐波激励下,分别采用传统等效方法与本文直接算法求解结构响应,对比结果列于表1和表2中,第1层和第10层结构响应的相平面图如图2、图3所示。
表1 简谐激励(ωg=2.5 rad/s)作用下的结构各层最大响应结果
Table 1 Maximum response results of each floor of the structure under harmonic excitation(ωg=2.5 rad/s)
图2 简谐激励(ωg=2.5 rad/s)作用下第1层和第10层结构响应相平面
Fig.2 Phase plane of structural responses at the first and tenth stories under harmonic excitation(ωg=2.5 rad/s)
表2 简谐激励(ωg=15 rad/s)作用下的结构各层最大响应结果
Table 2 Maximum response results of each floor of the structure under harmonic excitation(ωg=15 rad/s)
图3 简谐激励(ωg=15 rad/s)作用下第1层和第10层结构响应相平面
Fig.3 Phase plane of structural responses at the first and tenth stories under harmonic excitation(ωg=15 rad/s)
(1)两种时间步长下的三种响应计算结果基本一致,表明本文算法具有良好的稳定性与求解精度;
(2)当外激励频率较低,接近结构自振基频时,由传统算法所得的各层响应结果,相对于本文算法所得结果的偏差不大,三种响应的偏差均小于3%,图2所示的两种方法的相平面曲线基本一致;
(3)当外激励频率远大于结构自振基频时,由传统算法所得的各层响应结果,相对于本文算法所得结果的偏差较大,其中位移最大偏差接近8%,速度最大偏差接近16%,加速度最大偏差接近23%,图3所示的两种方法的相平面曲线差别较大。
在实际地震工程中,地震激励包含的频率成分较为复杂,结构响应是多个频率作用的综合结果。此处以El Centro(NS,1940)地震波为例,取地震动峰值加速度为200 Gal,采用传统算法和本文算法求解结构响应,相关结果如表3所示,另外在图4、图5中给出了第1层、第10层结构三种响应的前10 s时程(包含最大响应)对比,图6则给出了相应的响应相平面。
由表3可见,在两种时间步长下,本文算法所得三种响应计算结果仍基本保持一致。在实际地震激励下,传统算法相对于本文算法的偏差较大,其中位移最大偏差接近10%,速度最大偏差接近16%,加速度最大偏差接近19%。由图4和图5的时程结果也可见,传统算法与本文算法的位移结果趋势接近,峰值略有区别;而速度和加速度结果的趋势和峰值均有较明显差别。图6所示相平面也表明传统算法与本文算法结果存在较大偏差。
由此可见,在实际地震工程应用中,地震激励的多个频率成分对粘弹性阻尼器的性能影响不容忽略,高精度的结构响应结果可采用本文算法获得,相对地传统等效算法可用于定性分析参考。
表3 El Centro地震波作用下的结构各层最大响应结果
Table 3 Maximum response results of each floor of the structure under the El Centro seismic wave
图4 El Centro地震波作用下结构第1层响应时程
Fig.4 Response time history of the first floor of the structure under the El Centro seismic wave
图5 El Centro地震波作用下结构第10层响应时程
Fig.5 Response time history of the tenth floor of the structure under the El Centro seismic wave
分数阶导数模型可以较为精确合理地描述阻尼器的力学性能,但其中的Riemann-Liouville积分复杂,求解困难,一定程度上限制了该模型的广泛运用。而传统算法只根据结构基频,近似粘弹性阻尼器的等效刚度与等效阻尼,简化求解结构动力响应,忽略了结构高阶自振频率对阻尼器带来的影响,导致其计算精度不足。
本文针对含有分数阶导数模型的粘弹性阻尼器减震结构的运动方程,通过引入Caputo分数阶导数及Adams-Moulton求解技术,提出一种高精度的动力时程响应直接数值解法,方法计算思路简单,易于实现,求解精度高,稳定性好。本文直接算法对于外激励没有特殊要求,适用于任意激励情况的求解,可为有精密控制需求的含粘弹性阻尼器减震结构的动力响应提供高精度的计算结果。