板架式钢平台的结构形式：上部采用板架结构，共八层，平面尺寸为82.5 m×85.5 m（不包含局部外挑平台），顶层标高约68 m（不包括吊机）。甲板及墙板由图1所示的板材、大梁及扶强材组成，大梁采用T型钢，由于没有立柱与斜撑的影响，相比于框架结构可实现紧凑布置与缩减上部结构尺寸。结构在腿柱与甲板和墙皮连接处采用DH36/EH36加厚板材进行局部加强，底层甲板与下部导管架结构通过立柱钢管连接。导管架设计8个φ 2400的钢管主腿，成矩形布置，并在标高-13 m和-45 m处布置φ1400的水平横撑和φ1 200的X斜撑。导管架在主腿底部设置φ5060桩靴，与钢管桩采用水下灌浆方式连接。基础桩桩径4.5 m，桩长约130 m，桩重约840 t。板架式钢平台的材料属性如表1所示：

在满足仿真精度的前提下对原有模型进行简化：电气设备、电缆、通风管道等结构不属于承重受力结构，但其质量较大，在建模时通过质量点进行质量与惯性模拟。

板架式钢平台有限元模型见图2，桩基础采用PIPE16管单元模拟，水中导管采用PIPE59管单元模拟，上部甲板等采用 BEAM188单元模拟。PIPE59管单元和PIPEl6管单元是梁单元的一种特殊形式，同时支持大位移与大变形。载荷计算时考虑管外壁上的附着层，动力计算时附加质量计入附连水质量与管内、外附着质量。质量点采用MASS21单元模拟，各部件之间均为节点耦合连接。

图1 板架结构Fig.1 Plate frame structure

表1 结构材料属性Table 1 Material properties of structure

文中平台的环境荷载主要为波浪、海流与风荷载，由于波浪相位^[9]角对结构位移响应影响较大，需通过静力分析进行相位角搜索，分析时荷载入射角取90°，风速取25 m/s，波高取11.43 m，计算所得相位角与结构顶部中心点位移的关系曲线如图3所示。

图2 板架式钢平台有限元模型Fig.2 Finite element model of the plate and frame type steel platform

图3 相位角与结构顶部位移关系曲线Fig.3 The curve between phase angle and displacement at the top of the structure

由图3可看出，当相位角为81°时，结构顶部位移最大，最大值为0.051 m，应力云图如图4所示，最大等效应力为163 Mpa。为准确对比多种工况下结构位移响应和偏安全考虑，文中动力计算工况中波浪相位角均取值81°。

图4 平台等效应力云图Fig.4 The equivalent stress distribution of the platform

模态分析是研究结构动力特性的基本方法，可以判断具有刚度贡献的结构质量分布的均衡性与合理性，获取结构的自身振动特性^[10]。计算提取的板架式钢平台结构的前3阶频率与振型如表2所示。

表2 结构前3阶自振频率与振型Table 2 The natural frequency and vibration shapes of the former 3 step of the structure

波浪荷载是引起海上结构破坏和疲劳损坏的主要荷载。波浪和流荷载计算时应满足《港口与航道水文规范》（JTS145-2015）^[12]规范的相关要求。通过Morison方程计算小物体的波浪力^[13]，该方程可计算任意水深、波高和波长条件下结构的波浪力，并考虑波浪的非线性，其方程如下^[14]：

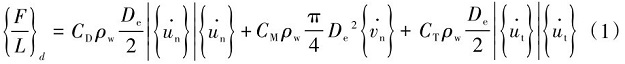
式（1）中：{F/L _d}为垂直于构件的单位长度的波浪力， N； C_D为法向拖曳力系数； ρ_w为水的密度， kg/m³；D_e为包括海生物在内的杆件的外径^[15]，m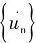； 为垂直于构件轴线水流速度矢量分量；C_M为惯性力系数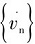； 为垂直于构件轴线水流加速度矢量分量；C_T为切向拖曳力系数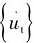； 为相切于构件轴线水流速度矢量分量。

不同规范中Morison公式水动力参数的取值如表3所示，参考港口与航道水文规范选取给定的C_D=l.2，C_M=2.0。海流荷载通过波浪水质点速度上叠加流速来计算，并考虑海流速度随水深的线性变化，实现海流荷载的准确模拟。

表3 不同规范中水动力参数Table 3 Hydrodynamic parameters in different standards

海流中，水质点的运动周期随时间变化缓慢，计算海流对结构物的作用力时，可把海流近似为稳定流动，假定海流对结构物的作用力只有阻力。考虑海流作用时，单位长度上圆管构件的海流力F_L可由式2计算^[20]：

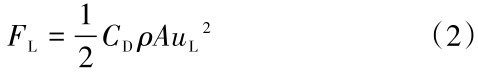
式（2）中：F_L为海流力，N；C_D为阻力系数；ρ为海水密度，kg/m³；A为单位长度构件在海流向的投影面积，m²；u_L为设计海流流速，m/s。

海洋环境中，波浪和海流是共同作用的，模拟分析时必须考虑波浪和海流的耦合。根据板架式钢平台的结构特点和仿真需求，选用ANSYS进行有限元模拟，ANSYS中PIPE59管单元支持考虑圆管形构件的流体静力、动力效应，可计算水中的圆管形构件的浮力、流力、波浪力的静载荷与动载荷。本文即通过PIPE59单元对导管架施加波浪与海流荷载，并通过水动力表定义与修改水流方向、波浪理论与相位角等参数。

板架式钢平台的风荷载需根据周年观测风速与理论公式计算，根据API RP 2A-WSD规范^[19]，作用在结构上的风荷载可按式3计算；

F=( ρ/2 ) (V )²C_sA（3）

式（3）中：F为风荷载，N；V为风速，m/s；C_s为形状系数；A为物体面积，m²；ρ为空气密度，取1.266 kg/m³。 C_s取值见表4。结构所在海域多年平均风速3.8 m/s，2008年9月24日受强台风“黑格比”影响时实测10 min平均风速34.6 m/s。

表4 风荷载形状系数Table 4 Shape factor of wind load

平台在前13种工况下参考点A点的位移响应极值如图6所示，各工况中位移响应极值均在响应趋于稳定时选取。

如图6所示，X向位移在入射角为0°时最大，在入射角为90°时最小，且入射角在（75°～105°）范围内，入射角变化对X向位移影响不显著，入射角由0°增大为75°时，X向位移降低11.90%，入射角由75°增大为90°时，X向位移降低44.86%。Y向位移在入射角为90°时最大，在入射角为0°时最小，入射角在（0°～180°）范围内，入射角对Y向位移影响显著，入射角由0°增大为90°时，Y向位移增大664.9%。综上，荷载入射角对结构位移影响显著，且对X向（强轴向）位移影响小于对Y向（弱轴向）位移的影响。

工况（1、7、14、15、16与17）中结构顶部位移响应如表6所示。由该表可以发现，当荷载作用方向由强轴向（0°）变化为弱轴向（90°）时，结构X向（强轴向）位移平均减小62.49%，结构Y向（弱轴向）位移平均增大765.37%。所以，当荷载作用方向与结构Y向（弱轴向）重合时，结构位移响应显著增大，对结构安全最不利。

当入射角为0°，流速增大100%时，X向位移增大19.0%，Y向位移增大9.1%，风速增大100%时，X向位移增大85.7%，Y向位移增大54.55%；所以当入射角为0°时，流速变化对结构位移影响不显著，风速变化对结构位移影响显著。当入射角为90°，流速增大100%时，X向位移未发生变化，Y向位移增大24.15%；当风速增大100%时，X向位移降低17.65%，Y向位移增大81.62%；所以当入射角为90°时，流速与风速变化对结构X向（强轴向）位移影响不显著，对结构Y向（弱轴向）位移影响显著。

图6 A点位移响应极值Fig.6 Extreme displacement response at point A

表6 结构动力响应Table 6 The dynamic response of the structure

图7 A点加速度响应极值Fig.7 Extreme acceleration response at point A

平台在前13种工况下参考点A点的加速度响应极值如图7所示。如图所示，荷载入射角对结构加速度影响显著。X向加速度在入射角为75°时最大，在入射角为90°时最小，且入射角在（0°～180°）范围内，X向加速度对入射角均比较敏感，入射角由0°增大为75°时，X向加速度增大175.94%，入射角由75°增大为90°时，X向加速度降低69.18%。

Y向加速度在入射角为90°时最大，在15°时最小。入射角在（0°～60°）范围内，Y向加速度对入射角不敏感，入射角由0°增大为60°时，加速度增大21.50%；入射角在（60°～90°）范围内，Y向加速度对入射角敏感，入射角由60°增大为90°时，加速度增大282.31%；

综上，荷载入射角对结构加速度影响显著，且对X向（强轴向）加速度影响小于对Y向（弱轴向）加速度的影响。

工况（1、7、14、15、16与17）中结构顶部加速度响应如表6所示。由该表可以发现，当荷载作用方向由强轴向（0°）变化为弱轴向（90°）时，结构X向（强轴向）加速度平均减小10.49%，结构Y向（弱轴向）位移平均增大396.55%。所以，当荷载作用方向与结构Y向（弱轴向）重合时，结构加速度响应显著增大，对结构安全最不利。

当入射角为0°，流速增大100%时，X向加速度增大10.0%，Y向加速度增大19.05%，风速增大100%时，X向加速度降低10.0%，Y向加速度增大4.76%；所以当入射角为0°时，流速与风速变化对结构X向与Y向加速度影响不显著。当入射角为90°，流速增大100%时，X向加速度增大17.6%，Y向加速度增大30.3%；当风速增大100%时，X向加速度不变，Y向加速度增大10.1%；所以当入射角为90°时，流速与风速变化对结构加速度影响均不显著。

由规范NORSOKS-002^[21]可知，海洋平台允许的最大加速度为2（m/s²），所以该板架式钢平台的加速度响应满足安全要求。