多次波是地震波场研究中普遍出现的一种干扰波,在地震勘探中指那些从震源出发到达接收点时经过一次以上反射波,包含了多次反射、折射、绕射等多种组合形势。海洋地震资料由于有海水的影响,往往形成与水面相关多次波,浅水表面多次波主要分为水层相关的多次波和非水层相关的多次波。当海水深度较浅时,水层多次波周期较短,容易与一次有效反射波混叠,压制较难。根据多次波是否发生在水层可以又可以细分为全程多次波和微曲多次波。而非水层相关的多次波通常周期较长,相对容易压制(图1)。
图1 多次波模型Fig.1 Multiple wave model
本文首先介绍了确定性水层多次波压制技术和基于波动理论的广义自由表面的多次波压制两类方法原理和适用性,通过和曲波域变换的理论相结合,在分析陆丰凹陷陆丰22洼多次波的成因及特征基础上,重点探讨不同技术组合减去方式在多次波压制应用效果。研究认为曲波域联合减可以在不损失有效信号前提下较好压制多次波,为获得保真地震数据奠定基础。
1.1 基于波场外推的确定性水层多次波压制技术
MOORE[6]等扩展了基于波场外推的方法,提出了确定性水层多次波压制方法(DWD),该方法利用自相关谱获得海底模型,可以用准确的振幅来预测水层相关多次波,但对于复杂海底难以适用。为此Kostov等[7]提出广义DWD方法,对于复杂海底多次波压制有明显优势。WANG[8]等也提出了类似的水底多次波压制方法(MWD),该方法压制效果明显但非常耗时,对于相对简单的海底情形来说,性价比过低,且无法压制与水层不相关的表面多次波。因此在实际资料处理中,海底较平缓工区一般采用传统的DWD方法即可以取得比较好的效果。
确定性水层多次波压制技术是先利用算法把水底有效反射信息计算出来,进而构建水层相关的多次波模型,然后通过自适应减法消除地震资料中与水底相关多次波。因此,在构建水底的有效反射时,需要知道水速以及水深先验信息。海水速度通过与温度、盐度和深度经验关系拟合得到,一般浅水区海水速度比较稳定近似为常数;水深可通过船载测深设备同步获得,然后利用格林函数模拟出水底有效反射波模型。再通过将它与原始地震数据的褶积构建出与水底相关的多次波模型。之后通过自适应匹配相减来进一步消除原始数据中与水底相关的各类多次波。值得注意的是该方法适用陆架浅水海底相对较平缓地区,且满足近似层状介质模型。同时在模型构建时炮检端都能产生水层相关多次波,为避免重复预测,在实际资料处理时一定要将重复的部分减去。
1.2 基于波动理论的广义自由面多次波压制技术
自由表面多次波压制方法是由Berkhout等[9]首先提出,2002年,Levin[10]根据近似NMO技术实现了零偏移距的3D自由面多次波压制,Van Dedem等[11]利用稀疏反演的方法进行了三维多次波预测。该方法基于波动理论,以先验速度模型或原始地震数据为驱动预测多次波,然后从地震数据中自适应减去,达到衰减多次波的目的。相比滤波方法,它对地下信息假设条件较少,在多次波模型预测中无需震源特征、表面反射的信息,也无需地下介质的任何信息,只需要含多次波的总波场就可以实现多次波的预测。
传统的自由表面多次波压制技术(SRME)假设采集的观测系统必须规则,有零偏移距数据,空间采样要足够,方位角要充足,且没有空间假频,实际上海上采集只有主测线方向满足这个要求。羽角漂移、采集空洞、船转向、近偏移距的丢失,都造成了不规则的空间的采样数据。数据的插值、外推、加密空间采样等方法,不仅增加了巨大的工作量,同时影响了数据的质量。广义的自由表面多次波压制技术(GSMP)克服以上传统的局限,它主要利用所观测到测线数据,对所有路径进行重建预测,进而准确识别出主反射。为了实现数据的准确估计,这就需要x和y两个方向都必须满足相同的采样间隔,而实际海上地震采集数据多为窄方位数据,联络线方向接收点位置简单、偏移距稀疏,因此在进行数驱多次波模型预测时需要尽可能多的数据输入,以确保区域多次波模型的稳定和准确。
1.3 曲波域变换理论
曲波变换是Candes等[12]提出的一种新的多尺度变换方法,该方法具有非常好的局部性、各向异性和很强的方向性,可以准确的表示图像的边缘特征,这种特性使得曲波变换[13-16]在地震处理噪音分离上具有广泛的应用前景。其实现过程首先是对地震数据 d( x,t ) 进行二维傅里叶变换D(k,w)=DFT [d(x,t) ],针对每一个方向,选择由一径向窗函数和频率窗函数联合构建新的窗函数Wn(k,w)对频率—波数域数据进行划分,且对所有方向n=1,…, N,必须使窗函数 Wn 都满足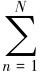 |w n ( k , w )|2,来保证地震数据完全重构,最终可以 得 到 每 一 方 向 的 曲 波 系 数 dcn ( x, t )=IDFT [ Wn ( k, w ) D ( k, w ) ]。曲波变换重构算法为曲波变换的反过程,首先求得某一方向的曲波系数,然后对所有方向曲波系数进行累加得到C ( k, w ),最后进行二维傅里叶反变换得到重构的数据R(x,t)=IDFT [C(k,w) ]。
|w n ( k , w )|2,来保证地震数据完全重构,最终可以 得 到 每 一 方 向 的 曲 波 系 数 dcn ( x, t )=IDFT [ Wn ( k, w ) D ( k, w ) ]。曲波变换重构算法为曲波变换的反过程,首先求得某一方向的曲波系数,然后对所有方向曲波系数进行累加得到C ( k, w ),最后进行二维傅里叶反变换得到重构的数据R(x,t)=IDFT [C(k,w) ]。
曲波变换的本质是将一系列频率—波速滤波器应用于时间—空间域数据,它具有不同频率、倾角或位置同向轴的能量。如果两个同向轴的频率、倾角或位置不同,那么它们在曲波域中将会被分开。因此,曲波变换可以实现多次波的自适应匹配相减[17-19]。在曲波域,当信号特征与曲波基形态拟合较好时,对应的曲波系数较大,反之则较小。在多次波模型预测过程中,利用曲波变换多方向的特性,实现了自由表面多次波模型构建。该策略减小了非平稳走时区域受多次波影响可能产生的假频对多次波模型的影响,具有更好的保幅性。
1.4 曲波域并联减多次波压制
传统的多次波压制方法主要是通过确定性浅水多次波和自由表面多次波模型的预测,然后进行最小平方匹配相减。其实现过程可以是逐步减去这种串联的方式[20],也可以是联合建模一次减去的并联方法。确定性浅水去多次方法主要利用多次波和一次反射有效波周期性的差异进行分离,但当地表条件复杂时,多次波周期性不明显,可分离性较低,压制也会不理想。自由表面多次波压制主要基于波动方程来预测多次波模型,以先验速度模型或原始数据驱动来预测多次波,然后从地震数据中进行自适应减去,达到压制多次波目的,相比滤波法,该技术完全由数据驱动,能够适应复杂地质条件多次波压制,但实际应用中会存在近偏移距数据缺失与自适应减损害有效信号的问题。可以看出串联减去的方式在参数选取不合适情况下容易造成有效信号的二次损伤,因此,针对浅水海洋资料处理,并联减的方式能一定程度保护有效信号,提高保真度。
多次波匹配相减法是一种自适应滤波法,主要求多次波和原始地震数据两者之间的最小平方差,当满足设定需求时就输出,否则就被压制。这种方法虽然在实际资料中应用广泛,但是由于正交性和子波差异一致性两个假定存在,匹配过程中可能会损失部分有效波或引入新的高频噪声,影响资料保真保幅性。为了更好地压制复杂地区多次波,近年来发展了曲波域匹配减。实现过程首先是与地震资料做子波匹配,然后将匹配的多次波转换到曲波域,之后进行曲波域反变换,最后采用定义阀值将匹配多次波去除。