基金项目:广东省自然资源厅科技项目(GDZRZYKJ2024008);国家级大学生创新项目(202410561152)联合资助。
作者简介:张搏翔(2002-),男,本科,主要研究边坡稳定性预警分析。
通信作者:宿文姬(1969-),女,博士,副教授,从事工程防灾减灾研究。E-mail:wjsu@scut.edu.cn
1.华南理工大学土木与交通学院,广州 510641;2.广东省地质环境监测总站,广州 510510
1.School of Civil Engineering&Transportation , South China University of Technology , Guangzhou 510641, China;2.Guangdong General Station of Geological Environment Monitoring , Guangzhou 510510, China
LSTM machine learning model;Finite element simulation;Finite difference method;Early warning and management
DOI: 10.13512/j.hndz.2024.02.08
我国国土辽阔,地质环境复杂多变,受人类工程活动和自然灾害影响,地质灾害易发频发。目前的地质灾害调查中对于边坡滑坡的易发性和危险性,原则上采用定量与定性相结合,其影响因素包括崩塌滑坡程度、水土流失状态、滑体体积、威胁人数和防治措施等。受限于实际工作中的条件,整体而言采用定性分析方法,定量分析方法采用较少[1-2]。
边坡稳定性计算的定量分析方法可分为极限平衡分析法和数值模拟分析方法两大类,极限平衡分析法的核心在于其建立的物理模型,实际应用中有Felleniue法、Bishop法、Sarma法等,根据不同的工程条件应用。但传统的极限平衡法利用大量简化计算使得滑动面不满足最基本的受力情况,且整体分析缺乏对于局部滑坡的稳定分析。而数值模拟分析法包括有限元(FEM)法、边界元(BEM)法、离散元(DEM)法,经过多年的发展目前有限元法得到了最广泛的应用[3]。
本文以广东省某地为例,对其中一处危险边坡进行有限元稳定性分析。根据前期调查数据报告,绘制出其边坡信息并进行有限元单元网格划分,后用FLAC3D软件进行有限差分法计算及边坡稳定性的计算,并找到该边坡临界失稳状态下的土体含水量。结合该处土体特性以及降雨情况,试给出边坡临界失稳时的降雨值。旨在对我国开展的地灾调查中边坡的危险性判定,以及预警降雨量提供参考。
本文边坡稳定性分析以有限元数模分析为基础,利用FLAC3D有限元软件进行稳定性迭代分析。FLAC3D分析软件以拉格朗日有限差分法为基础,赋以摩尔—库伦本构关系进行有限差分计算,相较于传统模型其对于边坡滑动情况模拟更加直观准确。
在工程实际中所建立的微分方程总是极为复杂,在现有数学水平下难以得出解析解,为了解决工程实际问题有限差分法[10]被提出。基于边坡的横向延伸稳定性不变,本文采用二维有限差分法进行分析。f(x,y)为二维空间某点的应力分量或位移分量,在二维空间内为连续函数。f(x,y)根据泰勒公式展开可展开成下列表达式:
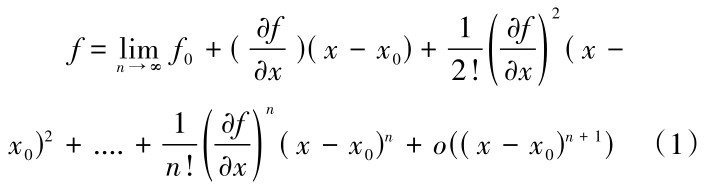
假定x→x0且考虑到幂级数三次幂函数以上数值极小以及工程应用实际精度要求,通常只需要展开至二次幂函数,即用f=f0 +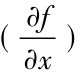 ( x - x0)+
( x - x0)+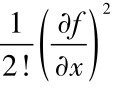 ( x - x0)2替代f即可。由简单运算可以得出混合偏导数的差分表达式:
( x - x0)2替代f即可。由简单运算可以得出混合偏导数的差分表达式:
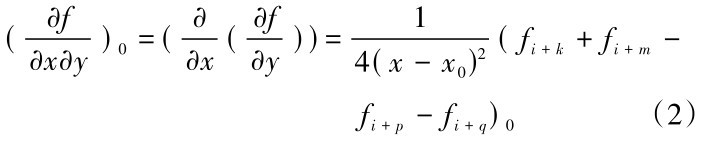
式(2)中fi+ k 、 fi+ m 、 fi+ p 、 fi+ q为fi相邻节点处的分量。根据上式可以将空间连续函数转化为相近点的差分函数,使得运算大大简化。
本构关系即差分量满足的某种关系,也称应力—应变准则。边坡稳定性分析满足摩尔—库伦准则,其基本表达式如下:
σij →M ( σij, eij, κ )(3)
式(3)中→为可用后边公式表示,M为某种本构关系(本文为摩尔—库伦关系), e ij为应变率分量; κ为一个历史参数;
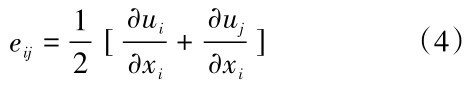
式(4)中ui为速度分量。
传统边坡稳定性分析有瑞典圆弧法和毕肖甫条分法等简化分析法则,而有限元分析系可以基于有限差分模型全面模仿边坡滑动情况进而进行精确分析。本文基于有限元强度折减法进行边坡稳定数值模拟,其基本示意图如下:
图1 边坡滑动受力示意图Fig.1 Slope sliding forces
根据力学平衡关系得:
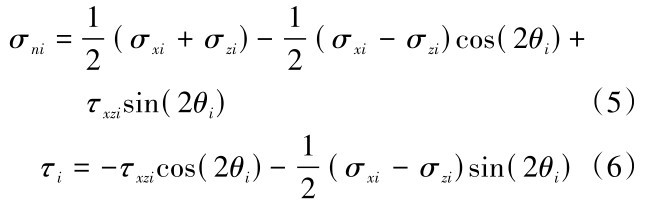
式(5)、(6)中σ ni为滑移面任意一点处法向正应力, σxi为该点x方向应力,σzi为该点竖向应力,θi为该点切线与水平方向夹角。
τfi =ci + σni tan ( φi )(7)
式(7)中τ fi为该点抗剪强度, c i为该点土体粘聚力, φi为该点土体内摩擦角
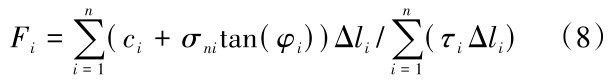
式(8)中Fi为该点安全系数, Δ li为滑移面弧段微元
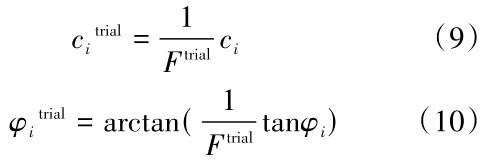
式(9)、(1 0)中Ftrial为迭代过程中的安全系数, cj t r i a l为迭代过程中的粘聚力,ϕj trial为迭代过程中内摩擦角粘聚力
由于土体本身难以产生压坏现象,因此在边坡安全性分析中主要考虑土体剪切强度,根据太沙基有效应力[5]原理,其基本公式如下:
τ=c' + σ'tanϕ'(11)
式(11)中τ为剪切强度,c'为有效粘聚力,σ'为有效压力,ϕ'为有效内摩擦角
长短时记忆网络[6-7](LSTM)是对于传统RNN (循环神经网络)的改进,可以处理传统RNN神经网络无法处理的长期依赖问题,其基本原理如图2所示。
图2 LSTM模型原理图Fig.2 LSTM model principle
传统的ARIMA、SARIMA、指数平滑模型通常在简单周期数据或规律性周期上升数据具有较好的拟合度,但对于非光滑曲线的拟合度较差;而LSTM作为改进的神经网络分析模型,对于长期数据以及非平滑规律性数据仍有较好的拟合优度。其主要包括:输入端、遗忘端、记忆端和输出端四个部分。
(1)输入端:其主要作用在于考虑当新信息输入时,何种信息应当被保留并更新状态,计算公式如下:
it =σ ( Qi⋅[ ht - 1, xt ]+ pi )(12)
C͂t =tanh( Qc⋅[ ht - 1, xt ]+ pc)(13)
式(1 2)、(1 3)中Qi是输入门的权重矩阵, pi是偏置项,xt是当前时间步的输入,ht - 1是上一时间步的隐藏状态。 σ是sigmoid函数(位于0~1之间), Qc是候选细胞状态的权重矩阵,pc是偏置项,tanh是双曲正切函数, C͂t代表目前信息对未来产生的影响。
(2)遗忘端:用来选择忘记哪些不必要数据,计算公式如下:
ft =σ ( Qf⋅[ ht - 1 , xt ]+ bf ) (1 4)
式(1 4)中Qf为忘记门的惯性权重, bf为偏置项。
(3)记忆端:主要目的在于记忆和存储信息,同时更新迭代状态,计算公式如下:
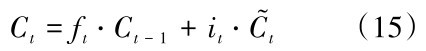
式(1 5)中ft为记忆门惯性权重, Ct为转移到下一步的信息。
(4)输出端:侧重于决定哪些信息应当被输出。
ot =σ ( Qo [ ht - 1, xt ]+ bo )(16)
ht =ot⋅tanh ( Ct )(17)
式(1 6)、(1 7)中ot为信息保留程度,趋向于1时信息保留较多,趋向于0时保留信息较少
训练模型拟合程度用R2表示,表示预测值中多少波动可以由自变量的波动来解释,其基本计算公式如下:
n∑( yi - fi )2 R2 =1 -i=1(18) i=1∑n ( yi - 1n∑i=1 yi )n
其中yi为模拟值,fi为实际值
利用matlab训练LSTM模型,其基本调试参数[8]如表1。
表1 LSTM模型部分参数表Table 1 Some parameters of LSTM model
利用训练好的LSTM模型训练2021—2024年(2024年仅包括1月份数据)年降雨量数据并进行预测得到图3、图4。
图3 误差分布直方图Fig.3 Error distribution histogram
图4 拟合优度曲线图Fig.4 Goodness of fit curve
由图像可知误差分布大致呈正态分布且拟合度R2=0.98,说明模型具有较高可信度。我们利用训练好的模型预测未来降水量并将真实值、拟合值绘制到图5。
从图中可以看出,自2021年以来全年降水量均有提升,且后期极大可能继续保持高位;模型在拟合优度方面达到0.998表明具有良好的拟合效果,说明我们的模型具有显著预测意义。
本文选取广东省某边坡进行边坡稳定性分析,基于前期实地调查报告获得边坡基本岩性土体情况并确定边坡影响范围,通过犀牛3D建模得到图6。
图5 预测未来两年降雨量曲线图Fig.5 Predicted precipitation curves for the next two years
图6 边坡建模图Fig.6 Slope modeling
其中最上层为砾(砂)质粘性土,下部依次为全风化黑云母花岗岩、强风化黑云母花岗岩、中风化
黑云母花岗岩,其基本力学性能如下表2所示。
表2 边坡土层与力学性能Table 2 Soil layer and its mechanical properties
利用饱和度、孔隙比、比重计算土体含水量的公式如下:

式(19)中wo为土体含水量;Sr为土体饱和度;eo为土体孔隙比;Gs为土体比重。
根据勘察报告数据和公式(15)可以计算得出暴雨工况和正常工况下土的含水量分别为34.1%和19.4%。
由于本文着重探讨未来降水量对于边坡稳定性影响情况,我们需要建立降水量与边坡力学参数的相关关系。目前国内大量专家学者选择用含水量作为中间传递变量[4,9]以此来建立物理量之间的关系;且利用FLAC3D进行有限差分法进行边坡安全系数迭代时需要的外界输入物理参数包括体积模量K、粘聚力c、剪胀角ψ、内摩擦角φ、泊松比ν、剪切模量G、抗拉强度σt、弹性模量E。根据太沙基理论与国内外学者研究[11],边坡稳定性着重考虑随含水量变化时粘聚力和内摩擦角的变化情况,因此其他输入变量以报告规范给定的数值范围为主而不做深入探讨。学者研究发现含水量与粘聚力和内摩擦角的变化大致为自然对数曲线或多项式函数曲线[4,9],本文借鉴前人研究成果经最小二乘法原则得到拟合图如图7所示。
从图7可以看出,随着含水量的增大粘聚力与内摩擦角均有所减小。根据非饱和土体的Fredlund抗剪强度公式:
τf =c' +( σ - u w ) tanϕ' +( u a - u w ) tanϕu (20)
式(20)中uw为孔隙水压力,ϕu为随( ua - uw)变化的摩擦角
含水量作用于孔隙水压力和随( ua - uw)变化的摩擦角来影响有效剪切强度,本文不做深入探讨,只关注最终有效剪应力变化。且其他物理量随含水量变化不明显,这里同样不再考虑。考虑到软件分析的需要将体积模量、剪切模量与弹性模量变换关系呈现如下式所示:
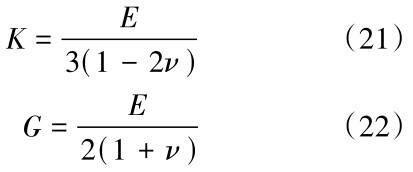
利用FLAC3D有限元分析软件通过数值模拟对土体进行从天然状态到饱和土体的状态进行边坡稳定性分析,得到土体在不同含水量状态下的边坡稳定系数如图8所示。
图7 部分物理参数与含水量关系Fig.7 Relationship between some physical parameters and water content
图8 边坡稳定系数与含水量关系Fig.8 Relationship between slope stability coefficient and water content
图9、图 10展示在饱和含水条件下边坡位移情况:边坡危险面主要集中于顶层土与全风化黑云母花岗岩层,下层中风化土通常不滑动。滑移范围内,滑移边界大致为弧形,与传统的极限状态平衡法相似。在滑移块中心位置沿坡底位移最大,因此预警治理主要在上两层进行且要注意坡中心位置稳定。
根据依据《滑坡防治工程勘查规范》(DZT0218-2006)及《岩土工程勘察规范》(GB50021-2001)进行稳定性评价
图9 边坡滑移面Fig.9 Slope slip surface
图 10 边坡沿坡底方向位移(蓝色区域最大) Fig.10 Slope displacement along slope bottom(the largest in the blue area)
表3 边坡稳定系数与稳定性关系Table 3 Relationship between slope stability coefficient and stability
图中框线为在边坡稳定系数处于临界值1.05时对应的含水量,为了简化运算与工程需要,本文认为总降水量与土体含水量呈正相关关系,因此临界稳定系数对应的临界降水量为24小时内累计降水量32.8 mm。
为验证模型对于危险日期预测的准确性,我们利用2020至2022数据进行学习并输出2023年预测数据。预测值与真实值情况如图 11所示。
图 11 验证2023预警降水量与实际情况拟合情况Fig.11 Fitting verification of 2023 precipitation by early warning with actual situation
图 11中可以发现在降水集中区域具有较好的拟合性。上文提及边坡稳定临界降水量为32.8 mm,因此我们着重探寻预测值是否超限降水情况与实际降水是否超限情况的拟合优度关系。利用两组数据(超限计为1,未超限计为0)进行比较分析,研究发现模型预测的预警日期与非预警日期与实际情况的一致率达0.8104且有15天与实际预警日期完全重叠,同时非完全重叠日期差距被控制在4天左右,表明二者重叠性较高,具有良好的预测精准度。
完成验证后利用LSTM训练模型预测的2024数据进行降水量搜索得到2024年警示日期如下表4所示:
表4 2024年部分预警日期Table 4 Partial early warning dates in 2024
从表中可以发现,预警日期主要集中在4月到9月份。研究还发现虽然10—12月份预警日期较前六个月份减少但仍有部分日期在预警日期内。应提前进行预防措施准备,例如刷坡护面、锚索锚杆支护、人工减小坡度等等。同样在暴雨时节,应提前提醒村民及时撤离危险点,避免造成人员伤亡。
(1)有限差分法弥补了微分方程缺乏解析解的局限性,从泰勒公式角度出发进行近似代替极大地简化了运算。
(2)LSTM模型改进了RNN算法,通过输入端、遗忘端、记忆端和输出端的自我学习达到R2=0.98的高强学习能力,对于未来降水预测具有重大的指导意义
(3)有限元边坡稳定性模拟分析解决了传统极限平衡状态受力不平衡、忽视边坡部分小变形的弊端,真实有效模拟了边坡滑动面并且计算了边坡稳定系数,得到了稳定系数随含水量变化力学参数的变化情况,进行了连续边坡分析。
(4)研究发现4—9月部分日期应着重预警,10—12月可能成为被忽视的滑坡易发期,可结合实际情况在此期内做进一步调查并采取相应防治手段。
总之,LSTM模型预测区域降水量结合FLAC3D对特定边坡情况进行稳定性分析,为基层的地灾防治提供了新的技术手段,然而现实中降雨年份具有不确定性,因此今后还应对模型加以改进以增大准确性。