在获取场地土质动力参数和评价场地土动力性能等方面上，岩土体剪切波速是极为重要的参考和分析依据。作为土动力学的重要参数之一，岩土体剪切波速被广泛应用在土木抗震工程中的方方面面，包括有场地土类别划分、住房用地防震规划、工程建筑地震安全性评价、场地砂土液化判别等工程项目，而岩土体剪切波速为这些工作提供了有力的数据支撑与评判标准^[1]。因此，众多研究人员通过分析研究岩土体剪切波速与深度之间的关系，为城市、建筑等实际工程项目提供了重要参考，为这些工程项目的顺利完成做出了不小的贡献^[2-4]。现如今场地剪切波速的获取方法多种多样，其中波速测井以其直接、有效、准确的优势成为使用最多的方法，但由于考虑到实际需要，如波速测井需要对测量地区进行打孔钻探工作，经费昂贵、资金消耗大，而且波速测井数据的数量及覆盖都十分有限，因此导致在对测井波速数据的应用方面上，研究人员们多集中在了对剪切波速、土地埋深、岩性等相互关系的探讨^[5]。因此，如果能够根据已有的钻孔资料并结合该地土层类别，给出剪切波速与土层埋深的经验关系，不仅可以得到该地区土层剪切波速的最佳预测模型和满足工程抗震设计和场地类型划分的剪切波速结果，还能节约成本、加快工程进度。所以，对于研究某一地区剪切波速与埋深之间关系的问题，到现今为止仍是具有实际需要和重大工程意义的研究课题。

国内外众多学者对该问题展开了一系列有意义的研究工作。如20世纪80年代，Lew等^[6]在仔细分析了土体的性质、物理状态和饱和度之后，提出了可以直观显示场地土剪切波速V_s与土层深度H之间关系的幂函数模型。国内也相继开展了大量的研究工作，曾勇^[7]分析了国内多地区的场地土层剪切波速资料、任瑞国等^[8]统计分析了山西临汾市的土层剪切波速资料、乔峰等^[9]基于河北廊坊地区的常规土类实测钻孔剪切波速资料，建立V_s经验公式，分析结果认为剪切波速与埋深之间存在相关性、土层深度是场地剪切波速重要的控制因素。何仲太等^[1]基于衡水市城区范围内的钻孔资料，主要采用线性函数模型，给出了衡水市城区常规土类剪切波速与土地埋深之间的统计公式；蒋其峰等^[10]通过收集鲁西平原地区工程场地钻孔的剪切波速资料，采用幂函数模型，得出了该地区常见土类的剪切波速与埋深间关系的经验公式；刘红帅等^[11]利用全国各地地震安全性评价工作积累的资料，在归纳整理了其中有关剪切波速部分的实测数据之后，使用数学函数公式中的最小二乘法分别以线性函数模型、指数函数模型和多项式函数模型，在两种情况下（区分场地类别和不区分场地类别）分别建立了全国范围内常规土类的剪切波速与土层埋深之间关系的统计公式。

天津地区是波速测井资料比较丰富的地区之一，由于许多重大工程场地地震安全性评价工作的开展和大量地震钻孔的开拓，天津地区拥有了数量众多且覆盖较好的测井资料^[5]。这些积累的资料为通过利用波速测井数据开展更为广泛的研究创造了有利条件，如王琦等^[12]在整理分析了天津地区地震安全性评价工作积累的有关实测剪切波速的数据资料基础上，通过使用幂函数模型建立了V_s经验公式，定性分析了常见土类剪切波速与土地埋深的相关性；高武平等^[5]利用天津滨海地区波速测井数据资料，研究分析了天津市滨海地区浅层剪切波速与基底构造的关系。本文运用天津市区实测剪切波速钻孔数据资料，经过统计分析，对天津市区第四系岩性和剪切波速及土层埋深关系进行探讨，旨在找到适用于天津大范围地区内的剪切波速预测模型及经验关系式，为天津地区工程抗震设计等提供参考的基础上，达到节约成本、方便快捷的目的。

利用上述关于剪切波速的统计分析方法，以分布在天津市不同区域的261个钻孔，共5961组剪切波速实测数据进行统计回归，得到了参与此次统计的天津市全部钻孔数据、中心平原区钻孔数据、滨海平原区钻孔数据的拟合关系式，以及得到了天津地区三种土类（粘土、粉土、中细砂）剪切波速与深度的统计关系。此次统计分析的剪切波速拟合结果如表1所示，剪切波速随深度拟合曲线如图3所示。

从图3可以直观清晰地看出，无论是区域位置不同，还是土体种类不同，天津地区的钻孔剪切波速都与埋深之间具有明显的相关性，而且是正相关。从对实测数据的三种拟合模型的曲线来看，天津地区土体埋深越深，剪切波速越大。无论从区域位置还是土体种类来看，剪切波速随埋深变深而增大的速度趋势逐渐减小（即埋深越深，剪切波速增速越慢），可以看出剪切波速随埋深而增加不是一个简单的增速不变的一次函数模型，而更符合增速随埋深逐渐变小的二次函数模型或幂函数模型（即土层剪切波速与埋深不是简单的线性相关，而是非线性相关）。从图3中可以看出，二次多项式拟合曲线在埋深大于100 m之后的剪切波速增长逐渐趋于平缓，与实测数据相比的误差较之于幂函数拟合曲线更小一些。因此二次函数拟合曲线相较于幂函数拟合曲线，在埋深大于100 m之后，更符合剪切波速的增长趋势。

考虑区域划分对场地土剪切波速与埋深间关系的影响，全部平原区、中心平原区和滨海平原区不分土类的场地土剪切波速与埋深间关系的拟合结果差异很小，R²均在0.9左右（表1）。根据第四纪地层厚度和沉积环境，天津平原区100 m左右埋深处为中更新统中上段地层。埋深70 m以上为全新统—晚更新统地层。这一时期，中心平原区为河流冲积、湖泊堆积、海洋沉积的交互沉积区；而靠近海岸的滨海平原区也主要为滨海相沉积与河流冲积相的交互沉积为主。沉积连续，且沉积差异小的特点使不同沉积分区间的拟合关系也相应的表现出差异小的特征。

将天津市的土类划分为粘土、粉土、中细砂共3类，用以探讨分析不同土类对场地土剪切波速与埋深之间的关系。其中各类土体的剪切波速与土层深度关系见图3，参数见表1。根据拟合结果发现：三种土类的剪切波速与埋深关系中，线性模型的拟合优度均明显低于二次多项式和幂函数模型。其中二次多项式模型在三种土类中都为推荐模型；不同土类的拟合优度差异较大，表现出土类粒径越小，拟合优度越高的特点；在相同的埋藏深度下，对于不同类型的土类，越是较大粒径的土类，其剪切波速越大。

表1 土层剪切波速与深度关系拟合结果Table 1 Fitting results of the relationship between the shear wave velocity and soil depth

根据不同沉积区的统计分析中，全区、中心平原区和滨海平原区不分土类的推荐模型均为模型二（即二次多项式模型），拟合优度R² 均达到0.93左右。而不同土类的拟合结果差异较大，其中粘土数据拟合优度最高的模型二的R²达0.9476。粉土数据的三种模型拟合优度R²在0.86~0.92，其中模型二和模型三拟合优度较高且相近；中细砂数据的三种模型拟合优度R²在0.72~0.75，其中模型二和模型三拟合优度也较高且相近。

图3 天津市不同土层剪切波速随深度变化拟合曲线Fig.3 Fitting curve of shear wave velocity with depth in different soil layers in Tianjin

综合不同沉积区和不同土类的统计，天津平原地区无论何种分类中，二次多项式模型的拟合优度都较为良好，可作为天津市平原区土体剪切波速与埋深间的关系推荐模型。具体经验关系式如下：天津市全区：V_s=72.713+7.1126H-0.0275H²；中心平原区：V_s=82.496+6.7505H-0.0246H²；滨海平原区： V_s =65.064+7.3827H-0.0295H²；粘土：V_s=74.744+6.6436H-0.0236H²；粉土：V_s=74.048+7.6152H-0.0319H²；中细砂：V_s=155.55+5.4919H-0.0195H²。

选取未计入统计的天津市平原区明俊创基中心的110 m钻孔资料和天津市滨海区渤海饭店的100 m钻孔资料（验证钻孔位置见图2）来进一步验证本文统计回归得出的经验关系式的可靠性和适用性。将使用本文推荐的区分土类和不分土类的模型二所得预测波速与实地钻孔探测剪切波速进行对比分析，分析过程中的相对误差为预测值与实测值之间的误差。两个钻孔每1m埋深选取一组数据，因为两个钻孔前两米土类为人工填土，故不将其纳入检验分析。因此，共选取明俊创基中心钻孔3～110 m埋深108组剪切波速实测数据，渤海饭店3～100 m埋深98组剪切波速实测数据。虽然所有数据全部预测得出结果，但因篇幅有限，以4m埋深为梯度，共选择明俊创基中心27组数据与渤海饭店25组数据列出，详细数据见表2~3。预测值均使用推荐模型二（二次多项式模型）获得，预测经验关系式分别为：粘土： V_s=74.744+6.6436H-0.0236H²；粉土：V_s=74.048+7.6152H-0.0319H²；中细砂：V_s=155.55+5.4919H-0.0195H²；不区分土类预测经验关系式为：V_s=72.713+7.1126H-0.0275H²。

通过验证结果发现，将利用本文的回归关系式推算出来的预测剪切波速值与实测剪切波速值进行对比，发现两者的误差较小，而且总体相对误差平均值控制在10%以内（表2~3）。但从两个表中列出数据可以看出，尚存在一些误差较大的结果。

表2 中心平原区检验钻孔的剪切波速与土层深度关系的预测结果与实测结果比较Table 2 Comparison between the predicted results and the measured results of the relationship between the shear wave velocity of the borehole and the soil depth in the central plain area

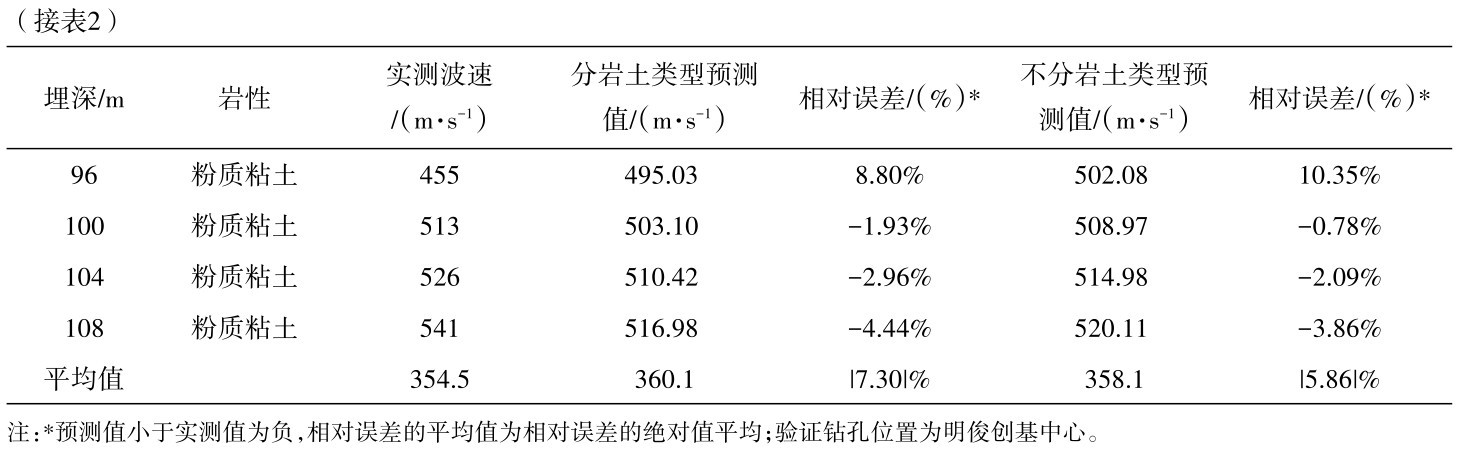
表3 滨海平原区检验钻孔的剪切波速与土层深度关系的预测结果与实测结果比较Table 3 Comparison between the predicted results and the measured results of the relationship between the shear wave velocity of the borehole and the soil depth in the coastal plain area

相对误差较大的预测值主要出现在0~30 m的浅表层，最大可达28.71%，而深度30 m以下剪切波速预测值相对误差显著减小，多数小于10%。浅部误差较大的原因受到多种因素影响：①根据天津市第四系地层资料，天津市沉积地层全新统底板埋深18.6 m左右，上更新统底板埋深69.9 m左右，在预测与实测的V_s-H关系图（图4）中可以发现，15~20 m左右实测曲线存在拐点。0~20 m波速曲线更陡，表明随土层深度增加，剪切波速并没有明显增大，这很好的匹配了全新统地层由于沉积时间较短，没有明显压实固结的沉积特征。而拟合曲线埋深20 m以下的中上更新统和中更新统地层部分，均经历更长时间的压实固结，表现出的特征更为一致。在拟合曲线中，大多数的数据均来自于埋深大于20 m的更新统地层。因此拟合曲线在0~20 m段的拟合优度偏低，导致相对误差较大；②在渤海饭店钻孔中，浅部（0~24 m埋深）的粘土层为淤泥质粘土，由于该种土类数量极少，因此被归为粘土型土类统计，也造成了预测值于实际值的较大偏差；③由于剪切波速随深度逐渐增加，而相对误差的计算方法，在预测值与实测值的相同差值相同情况下，由于深部剪切波速值基数较大而使相对误差百分比较小。

对于不同沉积区域，剪切波速值存在一定区别，表现为二次多项式拟合模型中的常数a差异较大，中心平原区为82.496大于滨海平原区65.064。因此在大多数情况下，相同深度和岩性情况下，中心平原区的剪切波速大于滨海平原区。这与沉积环境特征对应，在中心平原区以河流冲积和湖积的交互堆积为主，沉积物粒径相比滨海区域的滨海相沉积物粒径更大。在验证钻孔中，渤海饭店钻孔中，实测曲线的波动较为明显，这可能与滨海相沉积的沉积环境有关。因为滨海相沉积环境和滨海沉积物的情况较为复杂，其中既有陆源碎屑沉积，也会有潮间带的泥沙混合沉积物，甚至碳酸盐岩沉积。而中心平原区更为单一的沉积类型，使得实测波速曲线较为稳定。相应的预测值相对误差也更小。因此，区分不同沉积区域的剪切波速预测模型在天津地区可以提高预测准确性。

图4 预测与实测的Vs—H关系图Fig.4 The relationship between the predicted and measured Vs-H

对于同一钻孔数据，分土类预测波速和不区分土类预测波速与实测波速的相对误差非常接近，而总体数据相对误差的平均值不仅较为接近，甚至在明俊创基中心检验钻孔中，不区分土类的预测结果的准确度更优于区分土类的预测结果。因此，对于预测天津地区的剪切波速，区分土类与不区分土类预测差别不大，直接使用不区分土类预测模型可以更加简便快捷。从明俊创基中心与渤海饭店钻孔V_s-H关系图（图4）可以看出，预测值与实测值在整体上基本吻合，区分土类的预测剪切波速曲线与不区分土类的预测剪切波速曲线趋势非常相近，两条曲线都非常靠近实测值，这体现了不区分土类的剪切波速预测模型在天津地区也具有很大的适用性。

综合上述讨论，本文认为在天津地区可采用区分沉积区域、不区分土类的剪切波速预测模型进行剪切波速预测，具有较高的实用性和易用性。使用本文推荐模型预测出的剪切波速具有较高的适用性和可靠性，可供实际工程参考使用，但需注意浅层给出的预测值可能存在较大误差。

本文基于天津市场地剪切波速资料，对天津市平原区土层剪切波速与埋深间的关系进行相关性分析，主要获得如下结论：

（1）天津市土层剪切波速与埋深之间存在明显的正相关关系，而且剪切波速拥有随埋深变深增速变缓的趋势（即非线性相关）。天津地区的剪切波速预测推荐模型为模型二，获得了天津市区分沉积区域和不同土类的最优拟合公式。

（2）天津市平原区的第四系地层沉积特征与剪切波速结果相关性明显，浅层新地层拟合效果较差；同一埋藏深度下，受沉积环境影响，粒径大的沉积地层相较于粒径小的沉积地层，剪切波速更大。

（3）通过可靠性检验表明，区分土类与不区分土类预测结果的平均相对误差均在10%以内。在土类未知的情况下，使用不区分土类的拟合关系式进行剪切波速的预测可以获得较为合理的可靠性。

该研究结果可用于对天津平原地区土层剪切波速进行推测，可供天津市平原区的工程抗震等工作参考使用。