作者简介:杜斌(1987-),男,博士研究生,主要从事结构与岩土工程抗震技术研究。E-mail:dubin@live.com
1.中国建筑科学研究院有限公司地基基础研究所,北京 100013;2.中海石油气电集团,北京 100028
1.Institute of Foundation Engineering , China Academy of Building Research , Beijing 100013, China;2.China National Offshore Oil Corporation , Beijing 100028, China
Semi-underground LNG storage tank; Dynamic analysis; Fluid-structure-soil interaction; Multi-scale model
DOI: 10.13512/j.hndz.2023.03.18
备注
作者简介:杜斌(1987-),男,博士研究生,主要从事结构与岩土工程抗震技术研究。E-mail:dubin@live.com
引言
自2006年广东大鹏LNG接收站投入使用以来,我国大陆LNG储罐的数量已超过40座。然而,目前已建成的LNG储罐均为地上罐;在建的第一座半地下罐(22万m3)位于山东龙口,于2022年12月完成升顶;地下罐尚无应用业绩。实际上,与地上罐相比,地下罐具有更好的抗震性[1]等优点,其在国际上(以日韩为代表)得到了较为广泛的应用。
随着我国对LNG储罐需求的日益迫切,新工艺、新技术随之发展,半地下罐及地下罐的研究和进一步的工程应用成为必然。
LNG储罐可分为地上罐和地下罐,根据埋深的不同可进一步细分:全埋的情况(Under⁃ground)、只露穹顶的情况(Inground)、半埋的情况(Semi-underground,又称半地下罐)。
在LNG储罐的设计中,抗震设计是其中必不可少的一环。半地下LNG储罐的地震响应涉及储液—结构—土的动力相互作用问题,解决这一问题面临的最大困难在于缺乏地震发生时结构体系地震响应的实测数据验证。振动台试验是研究埋置结构地震响应的一个重要手段,通过振动台试验可以深入考察储液—结构—土相互作用体系的地震响应规律,获得结构的动力响应特性。对振动台试验进行数值模拟,并与振动台试验获取的时程结果进行对比,可验证数值模拟方法及相关参数取值的合理性和准确性,为发展半地下LNG储罐的动力时程分析法提供坚实支撑。
对于储液罐的抗震计算,储液—结构、结构—土的相互作用问题是其区别常规结构的特点。自1954年Housner[2]提出基于刚性罐壁假定解决液固耦合问题的弹簧质量模型以来,地上储液罐的抗震研究得到了很大发展。简化计算模型方面,以基于柔性罐壁假定的Haroun-Housner[3]模型、基于假定模态的Veletsos[4]模型等为代表。Nash等[5]基于附加质量的概念开发了储液罐地震响应分析的有限元程序,实现了液固耦合的模拟。Virella等[6]引入了声固耦合法用于储液罐的水平地震响应分析,Kianoush等[7]将之扩展到水平、竖向双向地震的情况,Rawat等[8]将声固耦合法的计算结果与试验结果进行了对比验证。国内,项忠权[9]课题组、孙建刚[10]课题组在地上储液罐抗震研究方面的专著具有代表性。地下储液罐的抗震研究方面,日本起步时间早(1970年已建成地下LNG储罐),工程实践和应用研究趋于前列[11-12],地下罐类型多为只露穹顶的情况。相较而言,我国半地下罐及地下罐的研究尚处于起步阶段,成果相对少[13-14],国内尚未见关于半地下罐地震响应数值模拟的报道。
本文在前期振动台模型试验研究[14]的基础上,基于大型通用有限元软件Abaqus,采用动力时程分析法,对振动台模型的试验工况进行数值模拟。针对半地下LNG储罐动力时程分析法中特有的技术要点进行阐释,如液固耦合、自由液面、多尺度模型、静动液压等。以期通过合理的模型简化与计算假定,在保证计算精度的前提下,降低建模难度、提高计算效率,并与模型试验结果进行对比验证,为进一步发展原型尺度的半地下LNG储罐动力时程分析法提供参考。
-
1 振动台模型试验
振动台模型试验在中国建筑科学研究院建筑安全与环境国家重点实验室的三向六自由度地震模拟振动台上完成,采用中国建筑科学研究院地基基础研究所(建研地基基础工程有限责任公司)设计研制的层状剪切试验箱装载试验模型。
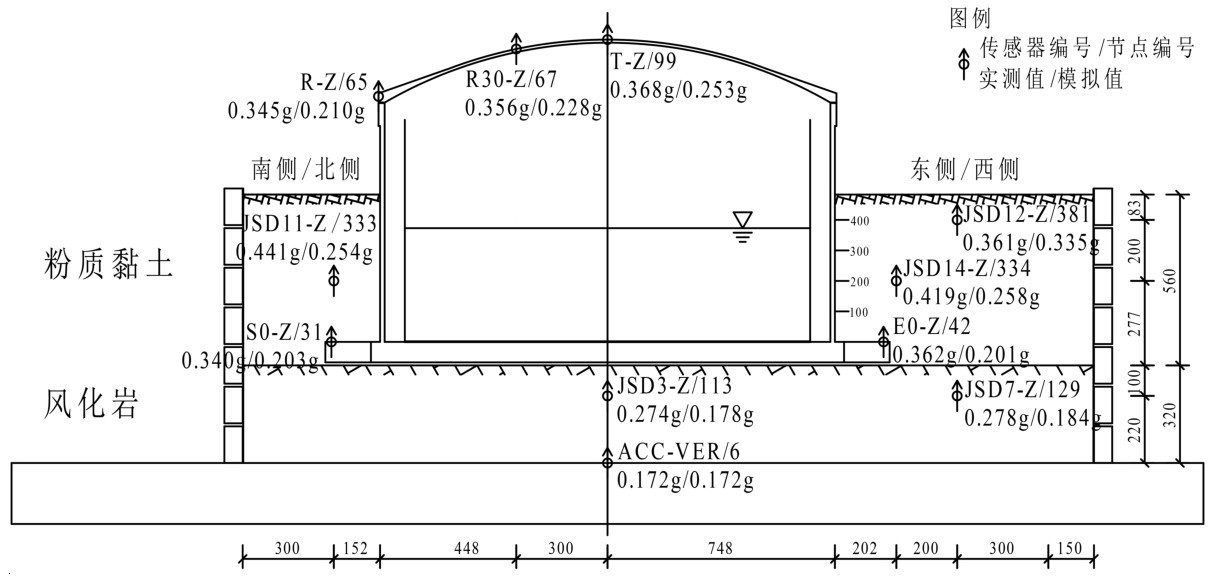
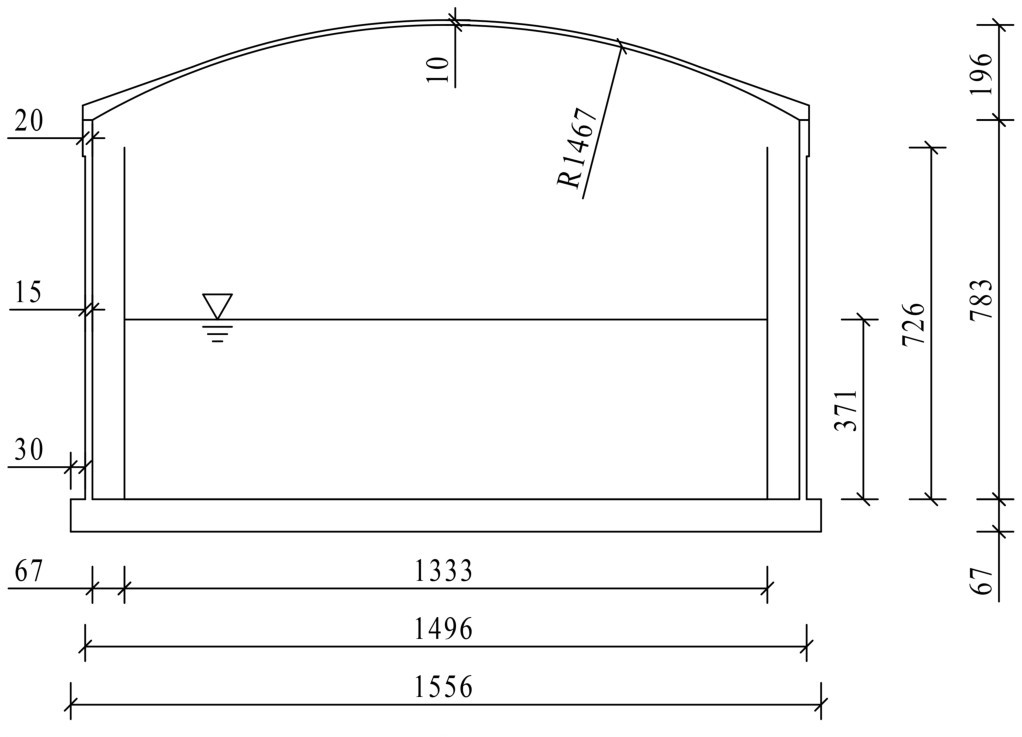
LNG全容罐模型参照某22万立方米LNG储罐进行简化缩尺。几何相似比为1/60,结构模型的立剖图见图1。
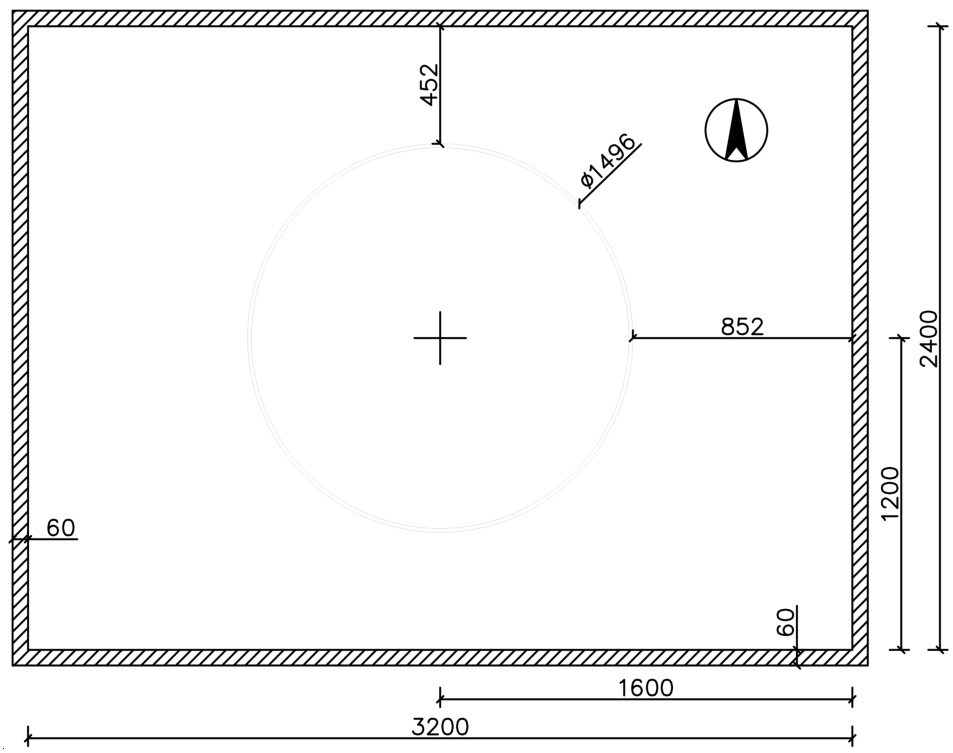
试验箱的平面净尺寸为3.2 m(纵)×2.4 m(横),结构模型置于试验箱中心位置,试验模型平面布置图见图2。
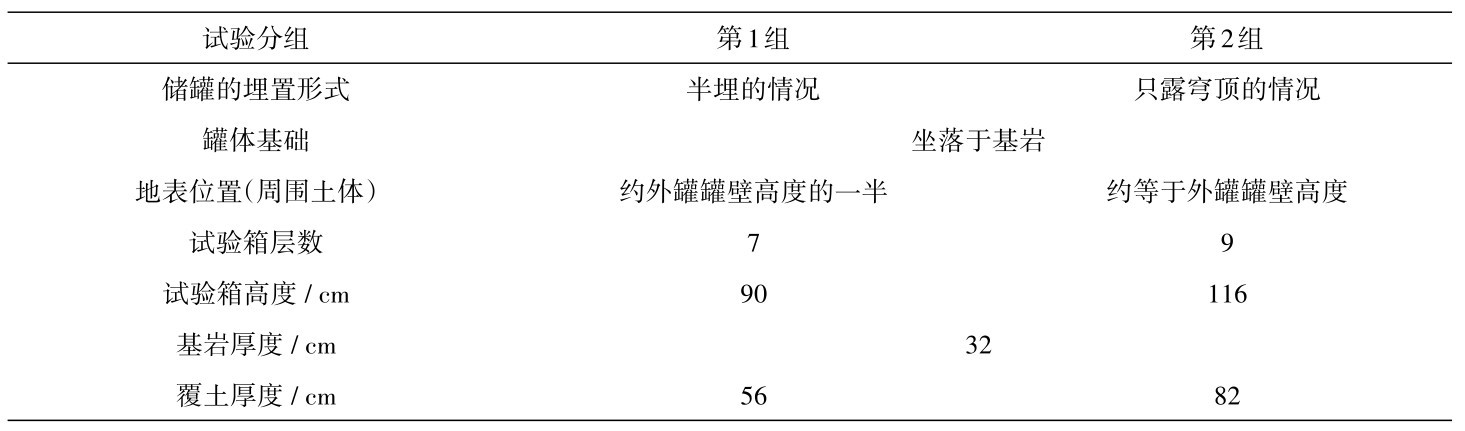
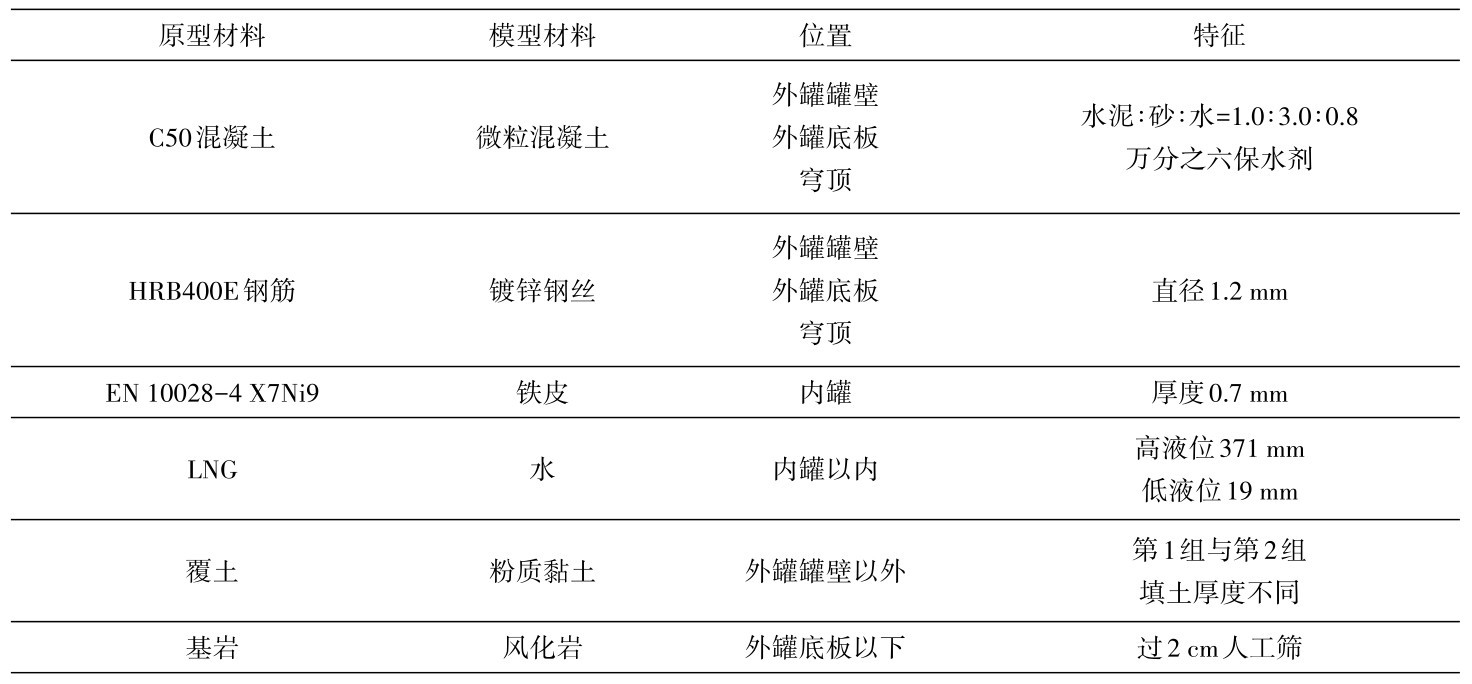
考虑不同埋深的影响,共制作1个结构模型、进行2组振动台试验,振动台试验分组及模型的对应关系见表1,不同分组的储罐模型的埋置形式见图3。振动台试验前按需装填土体、吊装结构模型、布设传感器,并按周围土体的装填高度调整层状剪切试验箱的层数。
图1 结构模型立剖图(单位:mm) Fig.1 Vertical section of LNG storage tank model (unit:mm)
图2 试验模型平面布置图(单位:mm) Fig.2 Plane layout of LNG storage tank model (unit:mm)
表1 试验分组Table 1 Grouping of shaking table tests
图3 储罐的埋置形式Fig.3 LNG storage tank model with different burial depths
第1组振动台试验完成后,增加层状剪切试验箱的层数,增高试验箱,然后在储罐结构模型周围继续装填土体至预设高度,并增设传感器,进行第2组振动台试验。振动台试验中采用的模型材料见表2。
表2 模型材料标准Table 2 Material specifications of LNG storage tank model
振动台试验采用2条真实强震记录的地震波(El Centro波、Mendocino波)以及1条人工波(安评波),地震动输入激励方向为水平单向(X)或水平+竖向(X+Z)。加载工况:2种埋置形式的LNG储罐× 2种液位(高液位、低液位)×3个地震动强度(0.25 g、0.75 g、1.25 g)。
-
2 有限元计算模型
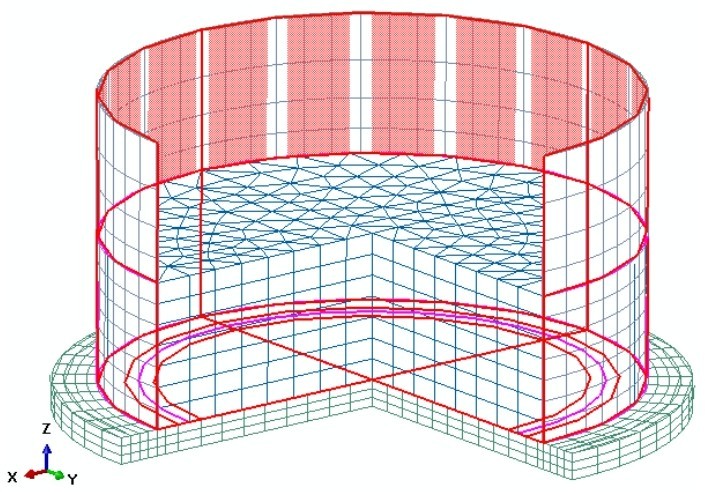
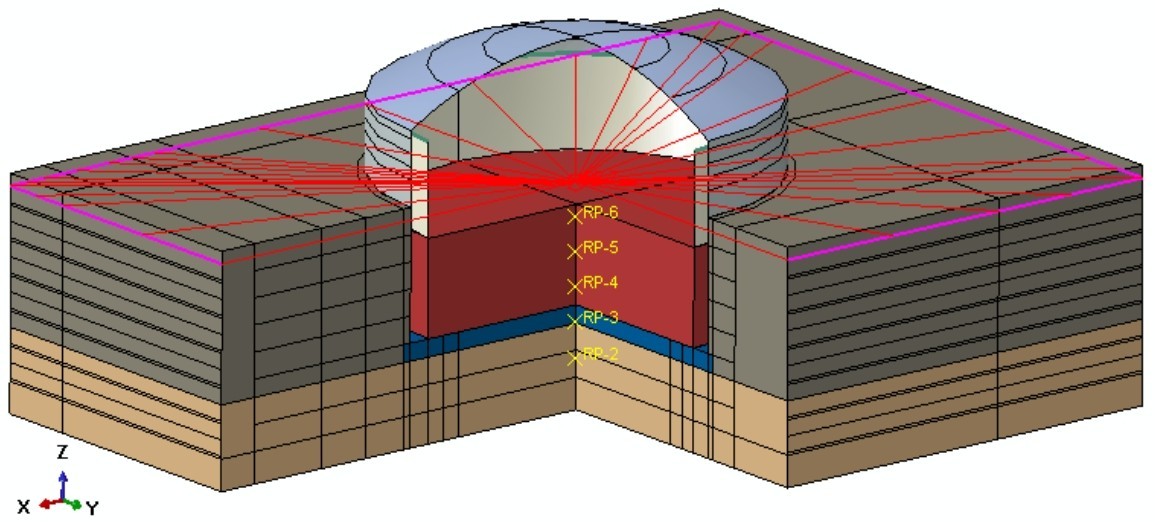
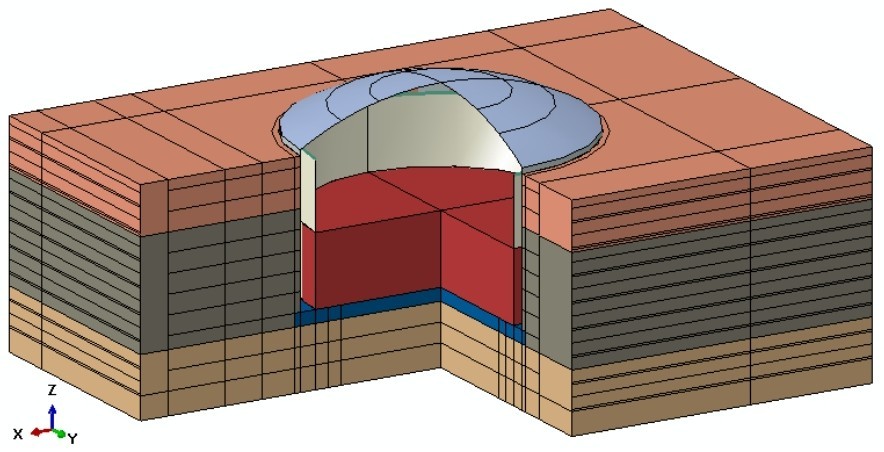
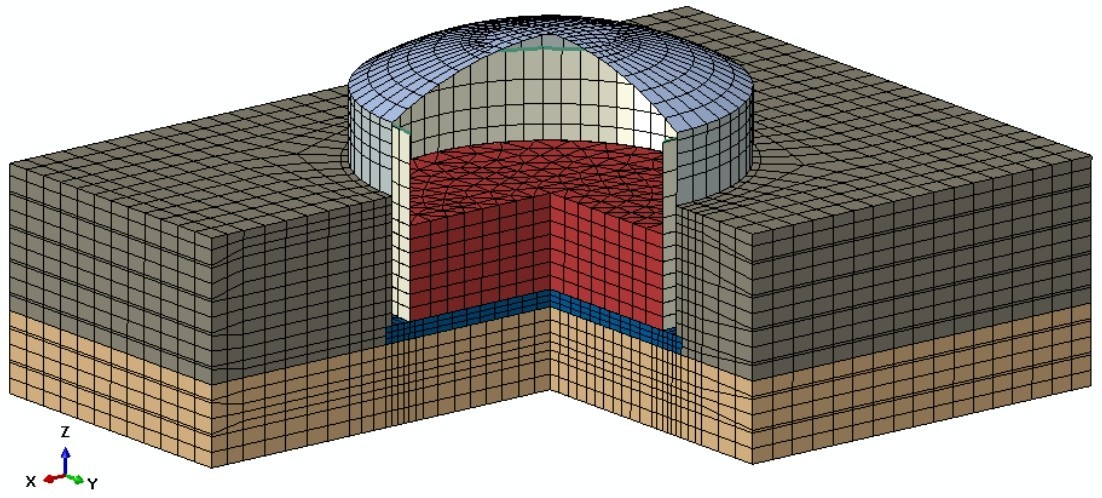
2.1几何模型基于振动台试验条件建立三维几何模型,如图4所示。几何模型包括储液、储罐结构、土体等三部分。因半埋的情况与只露穹顶的情况二者模型除埋深不同外,其他几何要素相同,受制篇幅,后续论述分析中仅以其一进行图示,实则对二者均适用。
模型的特征尺寸:外罐罐壁外直径1.496 m;外罐罐壁高度0.783 m,厚度15 mm;底板厚度67 mm,直径1.556 m;穹顶厚度10 mm;内罐罐壁直径1.333 m,厚度0.7 mm;罐体结构高度约1.055 m;储罐采用坐地式基础,直接坐落于风化岩。
坐标系:轴向为Z轴,+Z向与重力反向,坐标O点位于储罐底板底面的中心位置。+X向指东,+Y向指北。
单位制:吨(t)、米(m)、秒(s)。
土体和底板采用实体单元模拟,罐壁和穹顶采用壳单元模拟,储液采用声学单元模拟。
图4 几何模型Fig.4 Geometric model
2.2 时空离散对连续介质模型进行离散化产生的有别于连续介质模型中的波动传播规律的效应,是影响波动数值分析精度的主要因素。通过对离散网格模型中的时间步长、空间步距进行调整,能够在一定程度上减弱不利效应的影响,提高波动数值模拟的精度。杜修力[15]依据经验建议空间步距Δx可取:
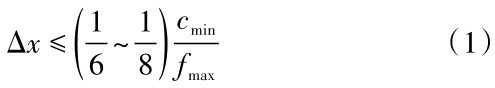
式(1)中:cmin为介质中的最小波速,fmax为输入波动能量最高截止频率。
对于声学单元,Abaqus软件建议空间步距不大于波长的1/10,最大为波长的1/6。即单元内节点的最大间距Lmax满足:

式(2)中: nmin代表一个波长内节点的最小数目,建议取nmin≥10;fmax代表激振频率;c为声速,可由c= Kf ρf计算,Kf为声学介质的体积模量,ρf为声学介质的密度。
在综合考虑计算成本和精度要求的基础上,确定计算模型的基本单元尺寸为0.1 m,分别对储液、储罐结构、土体等三部分进行网格划分,如图5所示。
对于高液位的情形,储液按设计高度建模,高度0.371 m;对于低液位的情形,储液不再参与建模。
对于半埋的情况,土体的总厚度为0.887 m,其中:风化岩0.320 m,粉质黏土0.567 m。
图5 计算网格Fig.5 Computational grid
对于只露穹顶的情况,土体的总厚度为1.140 m,其中:风化岩0.320 m,粉质黏土0.820 m。
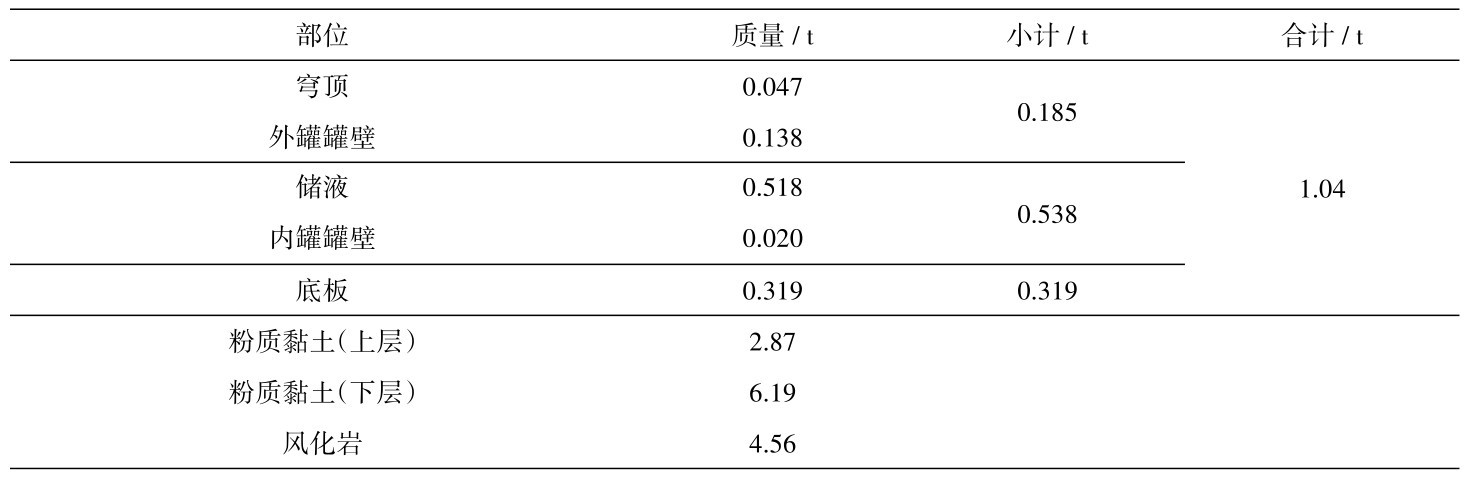
基于几何模型,各部位的质量统计见表3。对于半埋的情况,不含储液的总质量为11.28 t;对于只露穹顶的情况,不含储液的总质量为14.14 t。
表3 模型的质量Table 3 Model quality
基于有限元计算模型:对于半埋的情况,不含储液的总质量为11.28 t,储液的质量为0.51 t,合计11.79 t;对于只露穹顶的情况,不含储液的总质量为14.14 t,储液的质量为0.51 t,合计14.65 t。
对比可知,基于几何模型和基于有限元计算模型的质量差异小,后者略小。分析原因其差异来自于单元离散以折面等代曲面,在计算精度范围可视为二者一致。
值得注意的是,相比于储罐结构,储罐中储液的质量占比大,超过储罐总质量的一半,储液的合理建模是LNG储罐数值模拟的重要一项。
2.3 壳与实体的联结进行有限元分析时,往往依据结构特点采用不同类型的单元(如梁单元、壳单元、实体单元等),在保证计算精度的同时,可降低建模难度、控制计算规模、提高计算效率。然而,不同类型的单元之间往往存在过渡问题,又称为组合建模问题,如果不加以处理,单元之间就会存在位移不协调的情形,或无法正确传递力、弯矩、扭矩等。在结构领域,组合建模问题多见于多尺度模型[16]:不同构件的几何尺度差异显著。
对于大型LNG储罐结构,其罐壁(尤其是内罐罐壁)厚径比小,内罐罐壁的厚度尺度为10-2 m级,半径尺度为101 m级,往往采用壳单元模拟;而底板的厚度尺度为100 m级,往往采用实体单元模拟。由此,罐壁与底板的连接表现在有限元计算方面就是典型的壳单元与实体单元的联结问题。
对于壳单元与实体单元的联结,常用方法包括过渡单元法[17]、多点约束(MPC)法、平衡方程法,以及Nitsche方法[18]等。除基于力学的方法外,从工程实用角度出发,可通过特殊的建模方式解决壳单元与实体单元的联结,如将壳单元插入实体单元一定深度、在一定范围内设置刚性区等;相较基于力学的方法,该类方法经验性较强,计算精度不易控制。
Abaqus软件中的壳与实体的联结是采用基于表面的相互作用方法将壳单元和实体单元进行耦合,实现壳单元到实体单元的过渡。通过自动创建一系列的分布耦合约束,将壳单元的边线节点(作为参考节点)的运动与实体单元的表面节点(作为耦合节点)的运动进行耦合,并能够自动创建实体表面的耦合节点集合,适用于几何线性和非线性分析[19]。可以通过设置位置容差(position tolerance)和影响距离(influence distance)决定两个表面上的哪些节点参与耦合,示意图见图6。
图6 边线侧面的影响区域[19] Fig.6 Regions of influence for an edge facet[19]
大型LNG储罐结构,罐壁的厚度相对于底板的厚度较小,尤其是内罐罐壁,几何尺度相差约102级。为防止耦合权重因子为零,需要人工设置影响距离,保证实体表面上壳边线侧面(线)的两侧均至少各有一层单元面片参与耦合。
在本文的振动台试验数值模拟中,壳与实体的联结约束的影响距离设置为0.03 m,采用的关键词为:*SHELL TO SOLID COUPLING,INFLUENCE DISTANCE=0.03。
2.4 液固耦合Abaqus 软 件 中 的 CAS(Coupled Acoustic-Structure)方法,即声学结构耦合法,又称声固耦合法,系使用声波方程来描述振动波在流体中的传播。其中,流体域采用声学介质进行模拟,声学单元的每个节点仅有声压一个自由度。
对于可压缩、无黏流体,在小扰动情况下,其声学介质的平衡方程为:
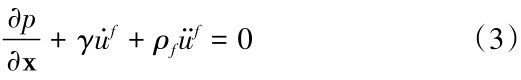
式(3)中:p为液动压力;x为流体质点的空间坐标;为u̇f流体质点的速度;üf为流体质点的加速度;ρf为流体的密度;γ为体积阻力系数(单位体积力与速度的比值,量纲FTL-4),用以描述声学介质中能量的耗散。
值得注意的是,除体积阻力项外,该方程与流体运动方程相同。因此,声固耦合法可用于含液容器的液固耦合分析[6],求解液固之间的动力相互作用。
假设流体是可压缩、无黏的,其声学介质的本构方程为:
p=-Kfεv(4)
式(4)中, Kf为体积模量, ε v=ε 1 1+ε 2 2+ε 3 3为体应变。
声学介质必须定义体积模量Kf和密度ρf。
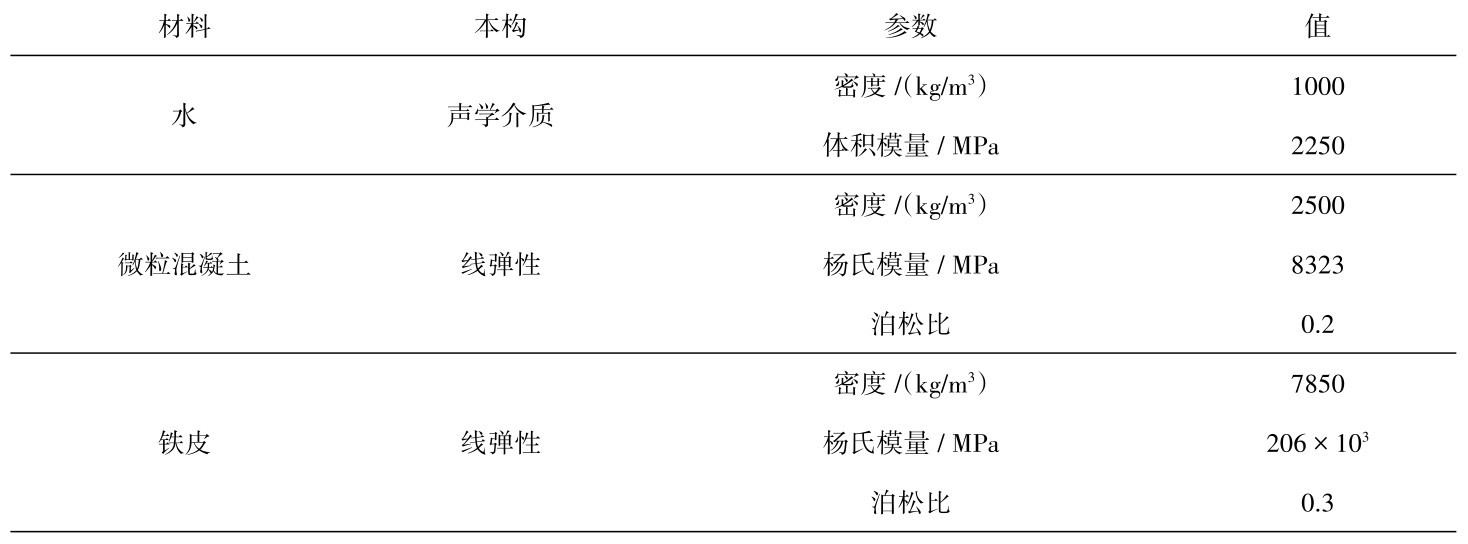
2.5 本构模型振动台试验中的水,数值模拟时采用声学介质;内罐材料铁皮采用线弹性本构模型;外罐材料微粒混凝土采用线弹性本构模型,模量由棱柱体抗压弹性模量试验获得,试块尺寸(mm)为70.7 ×70.7×212.1。
储罐模型材料参数汇总见表4。
土体的本构关系采用由南京工业大学陈国兴课题组提出的修正Martin-Seed-Davidenkov本构模型[20]定义,该模型基于Davidenkov骨架曲线的不规则加卸载准则,是能够描述循环荷载滞回曲线、遵从“扩展Masing法则”的非线性黏弹性动力本构模型,其应力应变关系曲线示意图见图7。
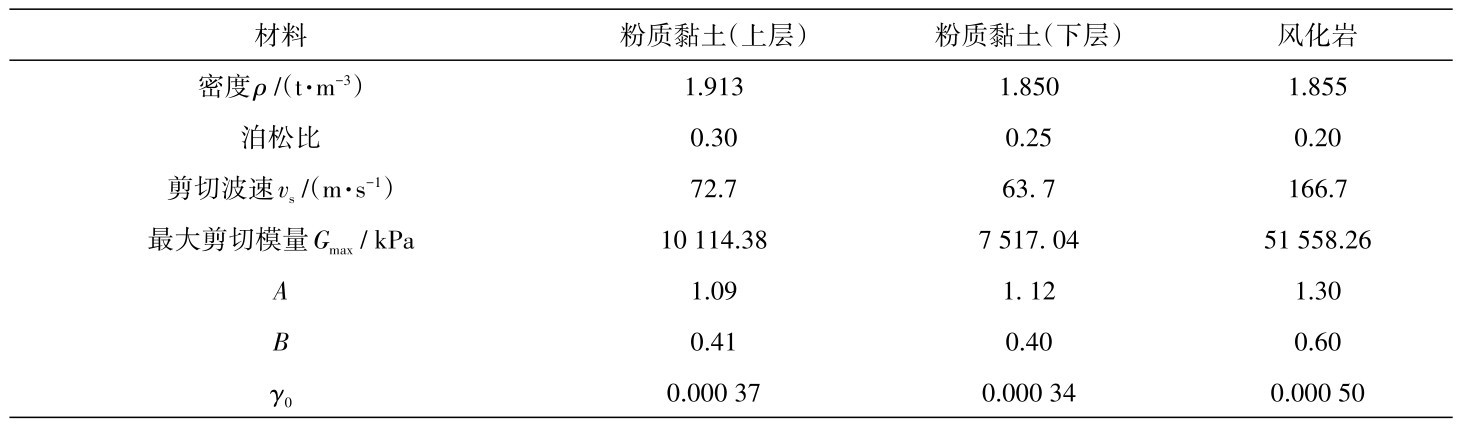
采用环刀取样的方式获取土样的密度ρ,将粉质黏土视为上下两层。将实测剪切波速取平均,采用实测剪切波速vs计算最大剪切模量Gmax:
G m a x =ρv 2s(5)
结合共振柱试验和相关经验数据,确定粉质黏土和风化岩的模型参数,取值见表5。
表4 储罐模型材料参数Table 4 Material parameters of tank model
图7 不规则加卸载准则修正的Davidenkov模型的应力应变关系曲线示意图[20] Fig.7 Schematic diagram of the stress-strain relationship curve of the Davidenkov model modified by the irregular loading-unloading criterion[20]
表5 粉质黏土和风化岩的模型参数Table 5 Model parameters of silty clay and weathered rock
根据振动台模型试验中的白噪声扫频结果可以获得模型系统的一阶自振频率和阻尼比ξ,取其平均值确定土体的Rayleigh阻尼系数:对于半埋的情况,αR=0、βR=0.000 88;对于只露穹顶的情况, αR=0、βR=0.001 10。
-
3 荷载与相互作用
3.1 液体的静压力Abaqus软件中的声固耦合法基于液动压力展开,不包括液体的静压力。并且,三维声学实体单元不支持重力、体积力类型荷载。因此,尚需人工施加液体的静压力。
借助Abaqus/CAE的解析场(Analytical Field)功能,可实现一种便捷的随空间变化的荷载施加方式:采用表达式形式描述场变量,自动生成标识符P的分布荷载(*DLOAD)。
若自由液面的高度为Z0,密度为ρ,重力加速度为g,那么,自由液面以下位置Z(即Z<Z0)的液体的静压力p0可表示为:
p0 =ρg (Z0 - Z)(6)
对于更为一般的情况,无需保证Z<Z0,位置Z的液体的静压力p0可表示为:
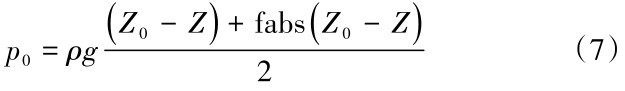
其中,fabs为求绝对值的函数。
3.2 液固交界面Abaqus软件针对声学介质与结构介质的交界面提供了两种建模方式:声学结构交界面单元、基于表面的相互作用。如果采用基于表面的相互作用的建模方式,结构、声学的网格需要具有不同的节点编号,而二者表面的网格可以在空间上不重合。比较而言,基于表面的相互作用的建模方式具有更好的易用性,且计算成本更低[19]。
储液与内罐之间的相互作用为液固耦合作用,使用基于表面的绑定约束(*TIE)定义之间的相互作用,离散类型为表面对表面(Surface to surface),位置容差(距离)为0.02 m。储液的外表面(环面及底面)指定为主面,内罐的内表面(环面及底面)指定为从面,如图8所示。
图8 液固交界面Fig.8 Fluid-structure interface liquid-solid interface
3.3 自由液面与晃动波高边界阻抗描述了声学介质压力和边界法向运动的关系。声学介质表面上任意一点的阻抗边界条件可描述为:
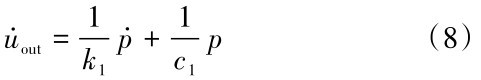
式(8)中:u̇out为声学质点沿声学介质表面外法线方向上的速度;1/k1为压力与表面的法向位移之间的比例系数,对应复阻抗的虚部,量纲F-1L3;1/c1为压力与表面的法向速度之间的比例系数,对应复阻抗的实部,量纲F-1L3T-1。
为模拟重力场环境小幅晃动情况的自由液面,体现重力作为晃动现象中主要恢复力的本质,可设置自由液面的边界阻抗[19]为:
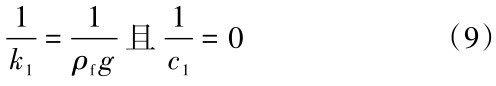
式(9)中,ρf为液体密度,g为重力加速度。
储液的自由液面采用边界阻抗的方式进行定义。采用的关键词为:*IMPEDANCE PROPERTY, DATA=ADMITTANCE。
自由液面离开原始(静止时)自由液面位置的垂直位移为晃动波高h,也称为波高函数。Abaqus软件流固耦合分析采用(ui,p)格式,流体域的节点自由度仅有压力p一项,无法直接获得流体域自由液面的位移,可用原始自由液面处的液动压力p计算晃动波高h。由于自由液面采用了线性小幅晃动假设,原始自由液面处的液动压力p与波高h成线性比例关系,有:
 3.4 模型边界
3.4 模型边界由于模型试验在能够模拟土体自由剪切变形的层状剪切试验箱内进行,试验过程中相互独立的层状矩形钢管框架能够模拟沿激振方向自由场地的变形,无需建立层状矩形钢管框架模型,仅将土体按框架所在区域进行分层处理,此时认为框架边界处相同高度的土体运动基本一致。
因此,在进行动力分析时,模型的边界条件设置如下:
(1)对于非底层的其他各层框架所在区域,采用绑定边界[21]:四侧边界相同高度的节点采用运动耦合约束,约束水平方向的平动自由度及三向转动自由度,约束控制点定义在各层框架所在区域的形心位置。对于约束控制点,仅保留水平激励方向(X向)的平动自由度。以第7层框架所在区域示例见图9。
(2)底层框架所在区域的四侧边界、底层框架高度内的分割面(模拟井字格)及底面边界直接输入沿激振方向的加速度时程。
(3)土层顶面自由。
图9 四侧边界示例Fig.9 Example of four-sided boundary
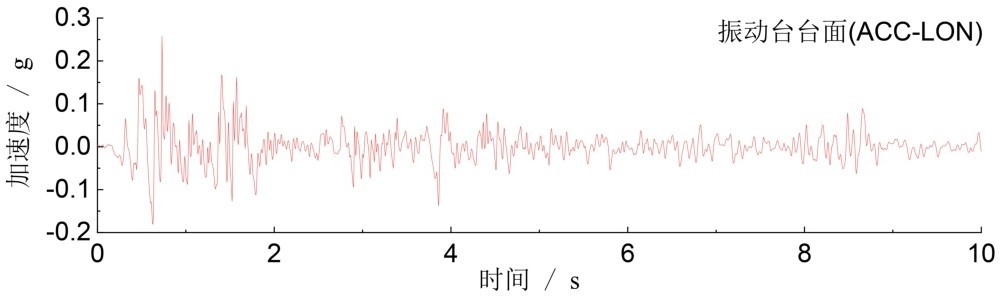
3.5 地震动输入加速度时程采用振动台台面的实测数据,采样频率256 Hz,计算时长取包含主要峰值点在内的10 s,不进行基线校正。对加速度传感器的实测数据进行滤波处理,滤波器类型采用Butterworth方法,高通,4阶,边界频率为0.1 Hz。
为便于对比分析,统一将El Centro波作为输入地震波,保持试验分组和工况次序编号与振动台试验一致。图 10给出了第1组(半埋的情况)、工况3、0.25g、X向、高液位的计算工况的输入地震动加速度时程。
-
4 计算结果分析
将振动台试验中传感器相应位置处的数值模拟结果与实测结果进行对比分析,验证数值模拟方法及相关参数取值的合理性和准确性。
图 10 输入地震动Fig.10 Input ground motion
整体计算模型:对于半埋、高液位的情况,单元25 630个,节点30 282个,自由度110 660个;对于只露穹顶、高液位的情况,单元30 614个,节点36 701个,自由度134 810个。
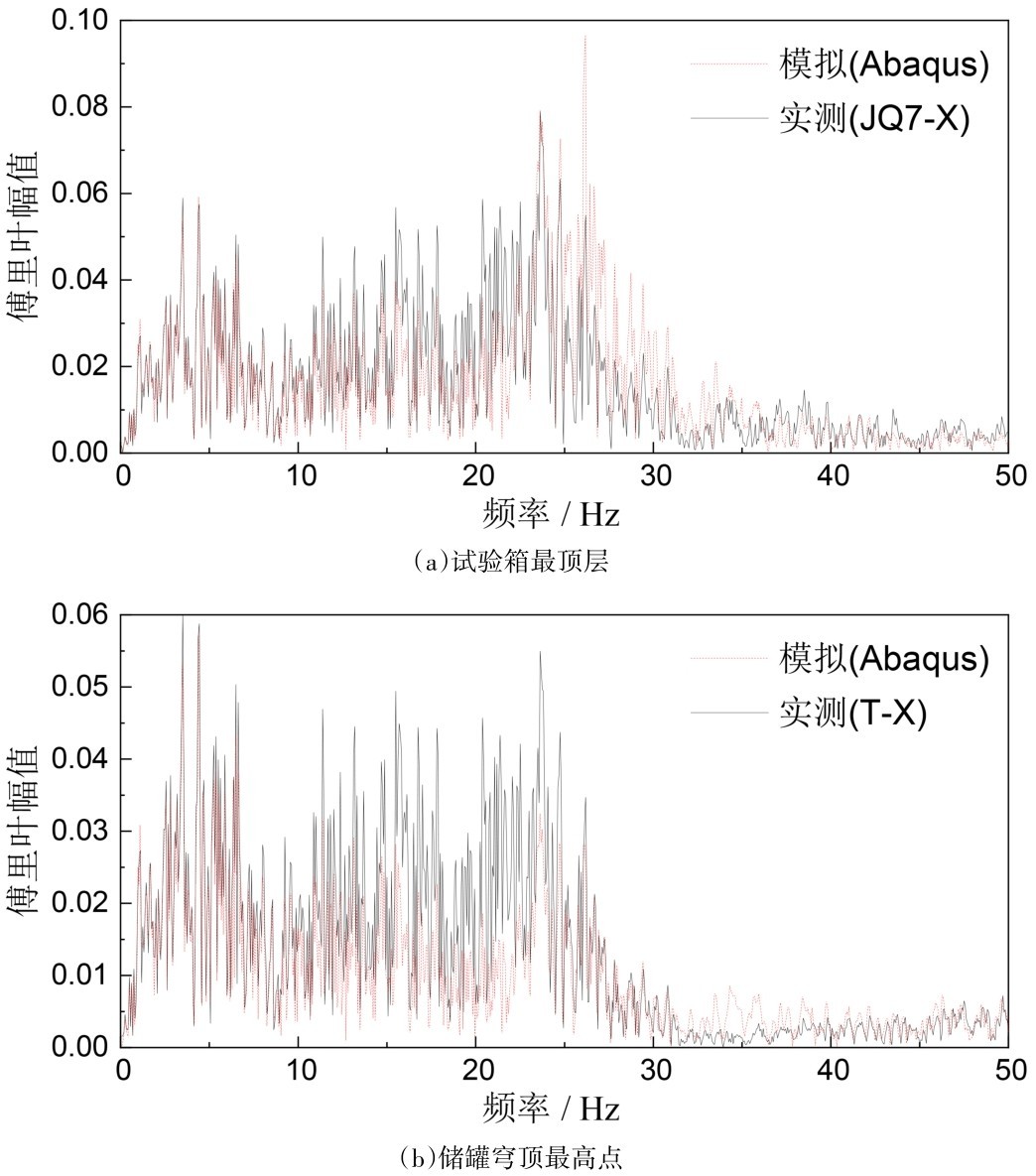
4.1 加速度响应图 11和图 12分别为半埋的情况(工况3、0.25g、X向、高液位)试验箱最顶层(第7层)和储罐穹顶最高点的模拟与实测加速度时程及傅里叶谱的比较。为保证制图效果,时程曲线仅展示包含主要峰值点在内的4 s,下同。尽管数值模拟结果与试验结果存在一定差异,但总体而言,二者在波形、频谱方面基本吻合,能够反映模型试验体系的动力响应规律和主要特征。
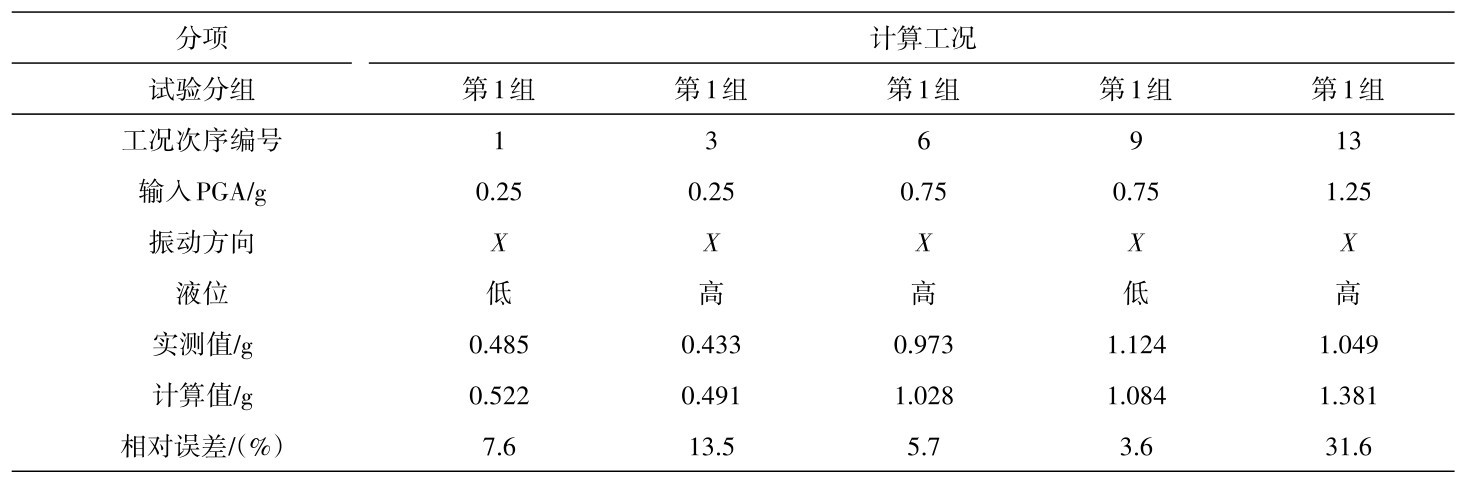
将不同输入PGA情况地表(试验箱最顶层)加速度峰值的计算与实测结果进行对比,结果见表6。对于加载次序居前的工况(0.25g)、居中的工况(0.75g),数值模拟的精度较高;随着逐级加载,居后的工况(1.25g),数值模拟与实测的差异增大。概与模型试验采用工况连续加载机制及参数取值方法有关:后续工况会受到先前工况累积效应的影响,而计算模型无法考虑这种情况;参数取值采用多次测量取平均的方法,均值与加载次序居中的工况的状态相当。
图 11 加速度时程的比较Fig.11 Comparison of acceleration time histories
图 12 加速度傅里叶谱的比较Fig.12 Comparison of acceleration Fourier spectra
表6 地表加速度峰值计算与实测比较Table 6 Comparison between calculated value and measured value of peak ground acceleration
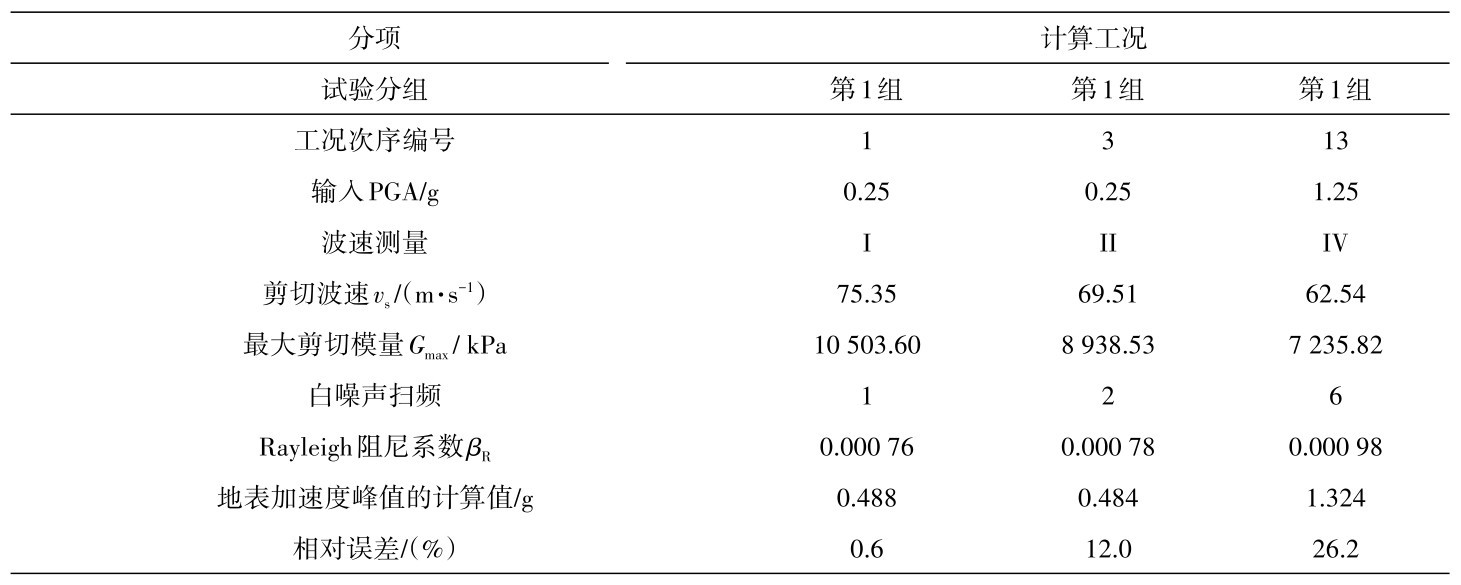
如前文所述,土体模型参数最大剪切模量Gmax计算取值时,实测剪切波速采用了取平均的方式;Rayleigh阻尼系数βR计算取值时,也采用一阶自振频率和阻尼比ξ的平均值。然而,实测数据[14]表明,在多工况的动力累积作用下,土体的剪切波速呈下降趋势,一阶自振频率呈下降趋势,阻尼比ξ呈上升趋势。因此,根据工况加载紧前的实测剪切波速计算最大剪切模量Gmax、实测一阶自振频率和阻尼比ξ计算Rayleigh阻尼系数βR,经调整的粉质黏土模型参数及计算结果见表7。将表6与表7的结果进行对比,结果表明:采用经调整的粉质黏土模型参数,地表加速度峰值的计算值与实测值可以更好地吻合,在一定程度上减小相对误差。
表7 经调整的粉质黏土模型参数及计算结果Table 7 The parameters and calculation results of the adjusted silty clay model
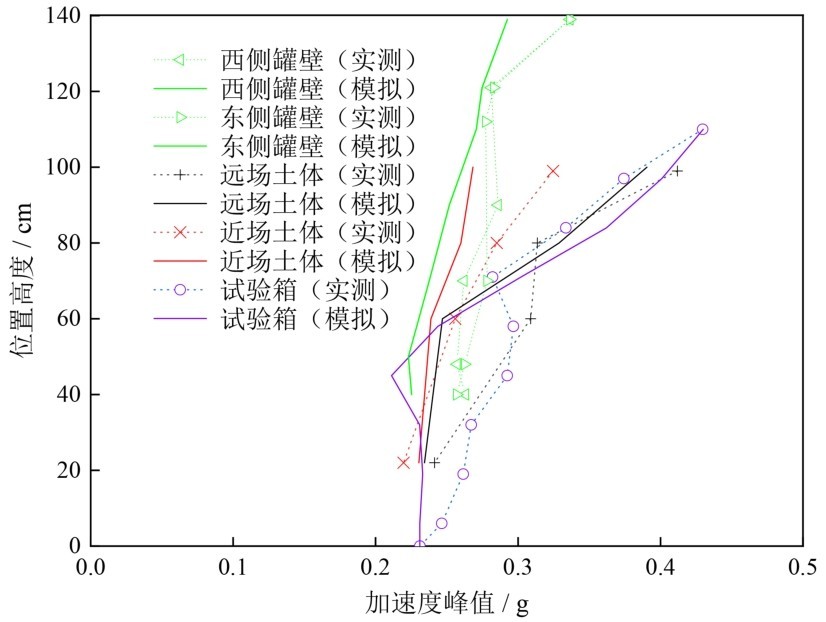
4.2 动力放大效应图 13给出了半埋的情况(工况3、0.25g、X向、高液位)土体和结构的加速度峰值随深度的变化曲线。可以看出:模拟与实测结果较为吻合;场地具有比较明显的动力放大效应;储罐结构与近场土体的加速度幅值较为接近;储罐结构及近场土体的加速度幅值小于远场土体的加速度,其原因可解释为储罐结构的刚度抑制了地震场地的晃动。
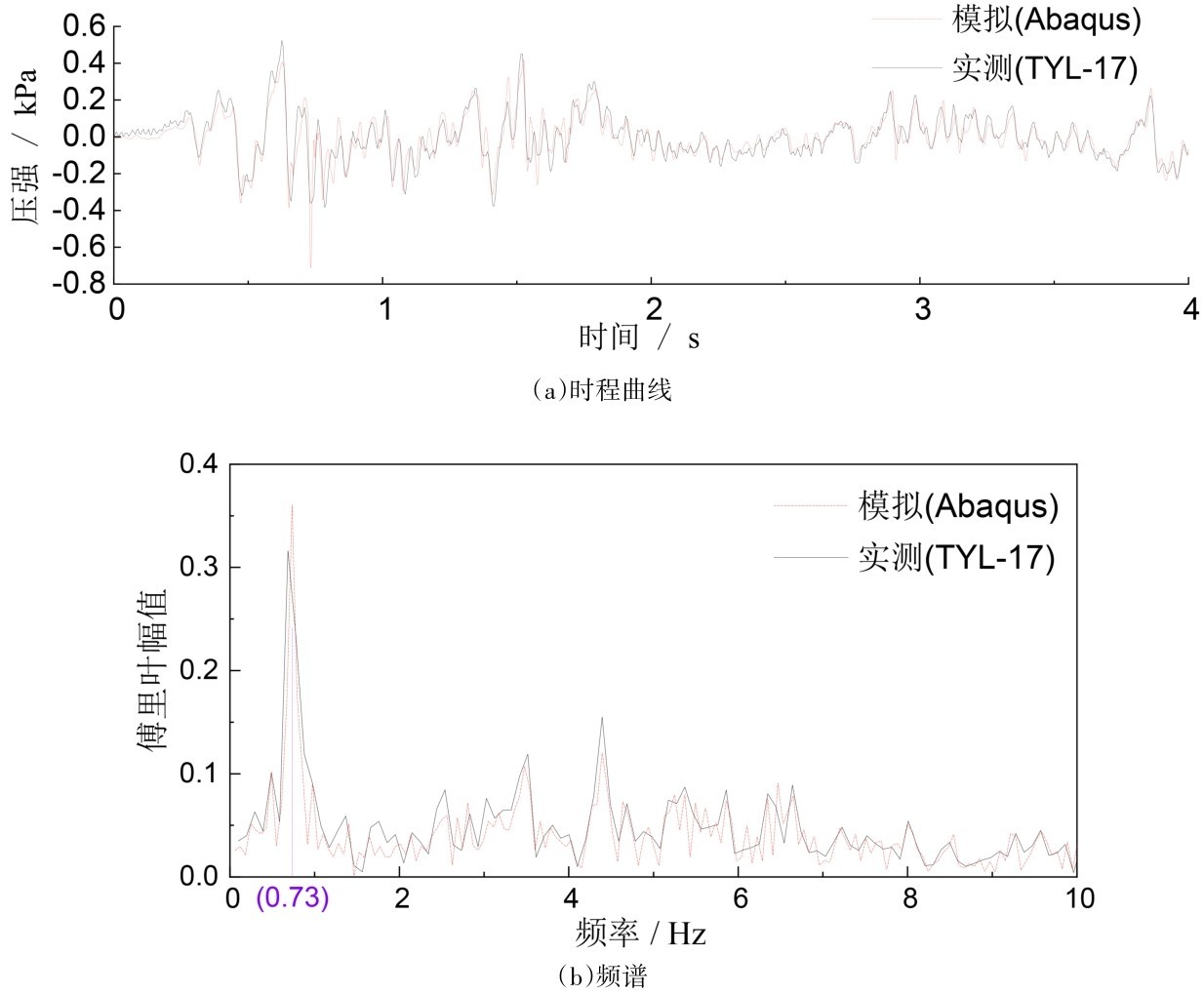
4.3 液动压力与晃动波高图 14给出了半埋的情况(工况3、0.25g、X向、高液位)监测点处的动水压时程与频谱,监测点(TYL-17)位于内罐底板内侧、距离内罐正东侧罐壁100 mm处。结果表明,动水压力的模拟结果和实测结果具有较高的一致性,采用声固耦合法模拟液固耦合具有可行性,精度较高。
图 13 动力放大效应Fig.13 Dynamic amplification effect
图 14 动水压的时程与频谱Fig.14 Time history and frequency spectrum of dynamic water pressure
图 15给出了半埋的情况(工况3、0.25g、X向、高液位)晃动波高的时程和频谱,晃动波高系根据式(10)由原始自由液面处的液动压力换算得到。可见,前两阶频率为0.73 Hz、1.40 Hz。
自由液面的晃动主要表现为环向谐波数n=1的反对称模态,在振动方向的边缘处出现波高最值。模拟所得晃动波高为-3.1~3.1 cm,这与振动台试验中罐内的视频摄像头捕捉到的正东侧水位线的波动范围34~40 cm(水位线位置高度等于静止水位线高度加晃动波高)相一致,见图 16。
采用Veletsos-Yang模型[22]计算液体晃动的第i阶频率fi:

式(11)中: λi为1阶第一类贝塞尔(Bessel)函数J1一阶导数的第i个根,λ1为1.8412,λ2为5.3314;R为储罐的半径;H为储液的高度;g为重力加速度。
对于振动台试验,根据式(11)计算可得:储液晃动的前两阶频率分别为0.73 Hz和1.41 Hz,与实测结果、模拟结果均相吻合。
此外,振动台试验中的另一个动态水压力传感器(TYL-18)位于内罐底板内侧、距离内罐正北侧罐壁100 mm处。因模型对称、边界条件对称,数值模拟所得动水压力均为小值(<0.001 kPa),亦与实测结果吻合。
4.4 埋深的影响图 17给出了只露穹顶的情况(工况3、0.25g、X向、高液位)土体和结构的加速度峰值随深度的变化曲线。埋入土体中的结构的加速度幅值与近场土体基本保持一致,储罐结构与周围土体几乎同时运动。越接近于地表,土体加速度峰值与结构加速度峰值二者之差越大,土体表现出明显的随高度的放大效应,而结构由于其自身刚度相对较大表现出了对土体地震动的抑制效应。土体距离结构越远,受结构刚度的影响越小。该现象亦与文献报道的日本山梨县的直径24 m、深9 m的地下钢筋混凝土储存罐(无水)在1976年6月16日5.7级地震中的实测结果[23]相一致。
图 15 晃动波高的时程与频谱Fig.15 Time history and frequency spectrum of sloshing wave height
图 16 自由液面晃动快照Fig.16 Snapshot of free surface sloshing
图 17 土体与结构的加速度峰值(只露穹顶的情况) Fig.17 Peak acceleration of soil and structure(only dome exposed)
只露穹顶的情况(图 17)相较于半埋的情况(图 13),因结构埋置更深,主体结构几近埋于地表以下,处于周边地层的握裹之中,储罐结构自身的振动特性难以发挥,储罐结构实则演变为一种具有环向土体约束的地下结构。
4.5 考虑竖向地震作用图 18给出了半埋的情况(工况5、0.25 g、X+Z向、高液位)监测点处的竖向加速度峰值。数值模拟结果与试验结果存在一定差异,相对误差较水平单向地震误差偏大;但总体而言,场地体现了竖向动力放大效应,储罐尤其是由罐壁和穹顶组成的大跨结构在竖向地震作用下动力放大效应较为明显,穹顶中心的加速度较穹顶边缘具有明显的放大。
-
5 结语
基于大型通用有限元软件Abaqus,以半地下LNG储罐振动台模型试验结果为基础,建立了考虑储液—结构—土相互作用的整体计算模型,对半埋和只露穹顶两种埋置形式的储罐模型进行了试验工况的数值模拟,并将模拟结果与模型试验结果进行了对比。结果表明:
图 18 竖向加速度峰值Fig.18 Vertical peak acceleration
(1)采用声固耦合法可以有效解决液固耦合问题,采用边界阻抗的方式定义储液的自由液面可以有效模拟自由液面的晃动,采用表达式形式描述的解析场可以便捷定义液体的静压力以弥补声固耦合法无法施加重力的缺陷,采用壳与实体的分布耦合约束可以有效解决罐壁与底板多尺度组合建模时的联结问题。
(2)考虑储液—结构—土相互作用的计算模型可以较好地模拟试验获得的加速度响应时程、动力放大效应、液动压力、晃动波高,为发展原型尺度的半地下LNG储罐动力时程分析法提供支撑。
(3)根据实测剪切波速和白噪声扫频结果对土体的最大剪切模量Gmax和Rayleigh阻尼系数进行调整,可在一定程度上减小误差,提高计算结果的准确性。
(4)具有一定埋置深度的储罐,其周围土体对储罐结构具有握裹作用,储罐结构因其自身刚度相对较大对周围土体地震动具有抑制作用。只露穹顶的情况相较于半埋的情况,储罐结构自身的振动特性难以发挥,储罐结构表现为具有环向土体约束的地下结构。
- [1]渋谷政文,池浦栄一. LNG地下タンクの現状と今後の動向[J].圧力技術,1991,29(2):88-94.
- [2] Housner G W. Earthquake pressures on fluid containers [R]. Pasadena,California:California Institute of Technology, 1954.
- [3] Haroun M A,Housner G W. Seismic design of liquid storage tanks [J]. Journal of the Technical Councils of ASCE,1981, 107(TC1):191-207.
- [4] Veletsos A S. Seismic effects in flexible liquid storage tanks [C]// Proceedings of the International Association for Earth⁃quake Engineering Fifth World Conference. Rome,Italy:IAEE,1974:630-639.
- [5] Balendra T,Nash W A. Earthquake analysis of a cylindrical liquid storage tank with a dome by finite element method [R]. Amherst, Massachusetts:University of Massachusetts, 1978.
- [6] Virella J C,Godoy L A,Suárez L E. Fundamental modes of tank-liquid systems under horizontal motions [J]. Engineer⁃ing Structures,2006,28(10):1450-1461.
- [7] Ghaemmaghami A R,Kianoush M R. Effect of wall flexibili⁃ty on dynamic response of concrete rectangular liquid storage tanks under horizontal and vertical ground motions [J]. Jour⁃nal of Structural Engineering,2010,136(4):441-451.
- [8] Rawat A,Matsagar V,Nagpal A K. Seismic analysis of steel cylindrical liquid storage tank using coupled acoustic-struc⁃tural finite element method for fluid-structure interaction [J]. International Journal of Acoustics and Vibration,2020,25 (1):27-40.
- [9]项忠权,李清林.立式储罐抗震[M].北京:地震出版社, 1990.
- [10]孙建刚,崔利富,罗东雨.大型LNG储罐抗震与隔震分析方法及试验[M].北京:科学出版社,2019.
- [11] Kaizu N,Mitsuo H,Koyama N,et al. Verification of seismic performance of in-ground LNG tank structures-study on streamlining by dynamic nonlinear analysis method [J]. Con⁃crete Library of JSCE,2001(38):1-32.
- [12]土屋智史,千々和伸浩,原田光男,ほか.近接するLNG地下タンク群と地盤で構成されるタンクヤード全体の3次元動的応答解析[J].土木学会論文集A1(構造·地震工学),2015,71(3):429-448.
- [13]肖立.大型LNG地下储罐受力变形试验及模拟研究[J].地下空间与工程学报,2020,16(S1):63-70.
- [14]杜斌,高文生,赵晓光,等.考虑埋深影响的地下LNG罐振动台试验研究[J].建筑结构,2023(53):1-11.
- [15]杜修力.工程波动理论与方法[M].北京:科学出版社, 2009:207-216.
- [16]孙正华,李兆霞,陈鸿天.大型土木结构的结构行为一致多尺度模拟——模拟方法与策略 [J]. 计算力学学报, 2009,26(6):886-892.
- [17] Karan S,Surana,Transition finite elements for three-dimen⁃sional stress analysis [J]. International Journal for Numeri⁃cal Methods in Engineering,1980,15(7):991-1020.
- [18] Takeki Yamamoto,Takahiro Yamada,Kazumi Matsui. Nu⁃merical procedure to couple shell to solid elements by using Nitsche’s method [J]. Computational Mechanics,2019,63 (1):69-98.
- [19] Dassault Systèmes. Abaqus Documentation [R]. Providence, RI:Dassault Systèmes Simulia Corp,2022.
- [20]赵丁凤,阮滨,陈国兴,等.基于Davidenkov骨架曲线模型的修正不规则卸载准则与等效剪应变算法及其验证[J].岩土工程学报,2017,39(5):888-895.
- [21]李嘉瑞,景立平,董瑞,等. ABAQUS模拟土-结构相互作用时人工边界的选取[J].地震工程与工程振动,2020,40 (3):174-182.
- [22] Veletsos A S,Yang J Y. Dynamics of fixed-base liquid-stor⁃age tanks [C]// Proceedings of U. S.-Japan Seminar on Earthquake Engineering Research with Emphasis on Life⁃line Systems. Tokyo,Japan:Japan Society for the Promo⁃tion of Earthquake Engineering,1976:317-341.
- [23]濱田政則.地盤耐震工学 [M].東京:丸善出版,2013:163-168.

![图6 边线侧面的影响区域[19] Fig.6 Regions of influence for an edge facet[19]](2023年03期/3期0018_figure_018_011.jpg)
![图7 不规则加卸载准则修正的Davidenkov模型的应力应变关系曲线示意图[20] Fig.7 Schematic diagram of the stress-strain relationship curve of the Davidenkov model modified by the irregular loading-unloading criterion[20]](2023年03期/3期0018_figure_018_014.jpg)