收稿日期：2022-10-12基金项目：基于大数据分析和地质-岩土-降雨耦合的降雨诱发型滑坡预警模型应用示范（湘财建二指[2019]19号）；遵义师范学院学术新苗培育项目（遵师XM[2021]1号-07）；遵义师范学院2021年乡村振兴项目（黔教合KY字[2016]018-5号）联合资助。作者简介：段中满（1975-），男，硕士，高级工程师，长期从事地质灾害监测预警、调查评价工作。E-mail：1002295900@qq.com通信作者：贾亮亮（1986-），男，博士研究生，副教授，长期从事地质灾害监测预警、调查评价工作。E-mail：451518464@qq.com
基于不同特征选择方法和随机森林法的滑坡易发性评价——以湖南中西部地区为例
1.湖南省自然资源事务中心，长沙 410118;2.遵义师范学院，贵州遵义563006;3.中南大学，长沙 410083;4.湖南容诚致远工程技术有限公司，长沙 410000
Landslide Susceptibility Assessment Based on Different Feature Selection Methods and Random Forest Method—a Case Study of Central and Western Hunan
DUAN Zhongman1，JIA Liangliang2,3，JIANG Mingguang3,4，LEI Yaobo1，CHEN Yana1
1.Hunan Center of Natural Resources Affairs ， Changsha 410118， China;2.Zunyi Normal University， Zunyi 563006， China;3.Central South University ， Changsha 410083， China;4.Hunan Rongcheng Zhiyuan Engineering Technology Co.， Ltd.， Changsha 410000， China
Landslide;Maximal mutual information coefficient;Recursive feature selection;Random forest
DOI: 10.13512/j.hndz.2023.02.13
备注
摘要
全文
图/表
参考文献
湘中、湘西地区是湖南省滑坡地质灾害最为频发的地区，同时该区旅游资源和自然资源丰富，是滑坡管理的重点区域。为研究湘中、湘西地区滑坡易发性评价模型的适用性，以湖南中西部地区为例，在初步选取的15个滑坡致灾因子的基础上，采用最大互信息系数、递归特征选择、基于随机森林的基尼不纯度指标和平均精确度指标等方法开展滑坡致灾因子优化，分析剔除了平面曲率和剖面曲率两个不重要因子，最终提取了13个重要因子，利用随机森林模型开展了研究区易发性评价，并采用最近两年滑坡数据开展验证。结果表明：不同特征选择方法优化后的滑坡因子结合随机森林模型所得的模型结果与实际情况吻合性较好，中、较高和高易发区滑坡占比77.58%，验证结果为79.58%，该模型对湘中、湘西地区地质灾害易发性评价模型选取提供了参考与借鉴。
The central and western Hunan is the most frequent area of landslide geological disasters in Hunan Province. At the same time， the area is rich in tourism and natural resources， and is the key area for landslide management. In order to study the applicability of the landslide susceptibility evaluation model in central and western Hunan，the historical landslides points and their corresponding features in central and western Hunan are taken as analysis data. Based on the 15 landslide disaster factors initially selected， the maximum mutual information coefficient， recursive feature selection， Gini impurity index based on random forest and average accuracy index are used to optimize the landslide disaster factors. Two unimportant factors of plane curvature and profile curvature are eliminated，and 13 important factors are finally extracted. The random forest model is used to evaluate the susceptibility of the study area， and the landslide data in the last two years are used for verification. The results show that the model results obtained by combining the landslide factors optimized by different feature selection methods with the random forest model are in good agreement with the actual situation. The proportion of landslides in medium， high and high prone areas is 77.58 % ， and the verification result is 79.58 % . The model provides a reference for the selection of geological disaster susceptibility evaluation models in central and western Hunan.
引言
滑坡作为我国最为频发的地质灾害，给人民的生产、生活及安全等造成严重威胁。湘中、湘西地区地势变化大，地貌复杂多样，山地、丘陵、岗地占80%以上，雨量充沛且十分集中，具备形成滑坡的有利条件，同时区内具有丰富的旅游资源与自然资源，对该地区的降雨诱发型滑坡进行超前预报具有重要的现实意义。滑坡易发性区划作为滑坡灾害风险管控的重要手段，可以清晰反应评价区不同区块滑坡发生的概率，对防灾减灾和土地开发利用有重要的作用。
滑坡易发性区划研究始于二十世纪七十年代中期[1]，经过近50年的发展，其方法和手段有了突飞猛进的发展，数据来源也越来越多样，评价因子也越来越细化，特别是近20年来，3 s技术和大量机器模型引入滑坡易发性评价，使得其成为当今滑坡地质灾害研究的热点，目前研究中使用较多的数据驱动方法包括：高斯过程（Gaussian Process， GP）[2]、支 持 向 量 机（Support Vector Machines， SVM）[3-4]、K最近邻（K-Nearest Neighbor，KNN）[5]、逻辑回归（Logistic Regression， LR） [6]、人工神经网络（Artificial Neural Network，ANN）[7]、随机森林（Random Forest，RF）[8-10]等。但由于滑坡致灾因子的复杂性和多样性，且不同地区滑坡数据的独特性，使得目前还未有一个普适的最优分析模型。滑坡致灾因子的选取是易发性评价的关键要素之一，然而目前滑坡影响因子的选择更多的是通过定性分析，缺少通过定量分析选择影响因子研究[11]。
本文以湖南中西部地区为例，在初选的15个致灾因子的基础上，采用最大互信息系数、递归特征选择、基于随机森林的基尼不纯度指标和平均精确度指标等方法开展滑坡致灾因子优化，提取了13个重要因子，结合随机森林模型，建立区域滑坡易发性评价，并开展成果验证以分析评价模型的准确性和实用性。
-
1 研究区概况
研究区位于湖南省中西部地区，包括娄底市新化县、常德市桃源县、益阳市安化县和益阳市桃江县，面积15 212.51 km2。研究区属中亚热带季风湿润气候，四季分明，雨量充沛，雨季为每年的4～10月，为湖南省的汛期。研究区总体南高北低，中部和南部山地和丘陵相间，向北逐渐过渡为洞庭湖冲积平原。滑坡主要集中发生在6～8月，占滑坡发生总数的85%，其中6、7月发生量占滑坡总数的75%，与降雨集中期基本吻合，但有一定的滞后性。
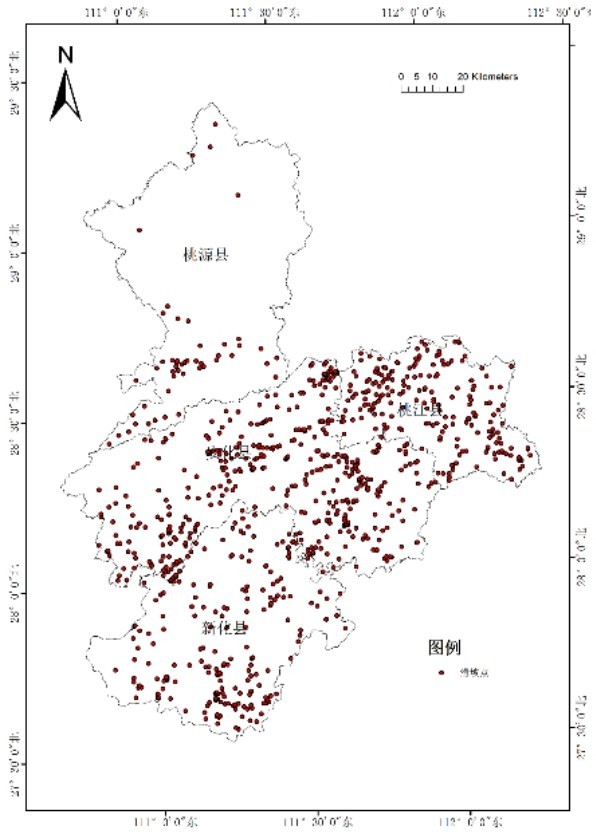
根据研究区各县自然资源局地质灾害统计成果，截止2022年12月，研究区发生的滑坡共1017处（图1），总体呈北东向展布，主要分布于安化县、新化县和桃江县，在桃源县南部有少量分布，其中土质滑坡占74.02%，碎石土滑坡占19.7%，岩质滑坡占6.28%。从滑坡体厚度上看，研究区发育有浅层滑坡（滑坡体厚度小于6 m）和中层滑坡（滑坡体厚度6～20 m）两种滑坡类型，其中浅层滑坡数量大，占比高，占总数的98.3%，中层滑坡数量少，占统计总数的1.7%。从滑坡体积规模看，小型滑坡占99.49%，中型滑坡占0.51%。
图1 研究区滑坡点分布图Fig.1 The distribution map of landslide points in the study area
-
2 计算方法
2.1 最大互信息系数最大互信息系数（Maximal Information Coefficient， MIC）是Reshef[12]提出的一种新的相关性度量方法。该方法基于互信息进行改良，相较互信息来说具有更大的普遍性和公平性。滑坡条件因子的最大信息系数计算公式如下：
式（1）中：B是一个关于样本规模n的函数，通常情况下B=n0.6；I ( D, X, Y )是指落入网格区域D的最大的互信息值；MIC的数值范围为[0，1]：当MIC=0时，代表X与Y变量之间相互独立；当MIC=1时，代表X与Y变量之间存在某种类型的函数关系。
2.2 递归特征消除递归特征消除[13]针对特征含有权重的预测模型进行，通过递归的方式，不断减少特征集的规模来选择需要的特征。实现过程如下：①给每一个特征指定一个权重，接着采用预测模型在这些原始的特征上进行训练；②在获取到特征的权重值后，对这些权重值取绝对值，并将最小绝对值剔除掉；③按照上述步骤，不断循环递归，直至剩余的特征数量达到所需的特征数量。上述过程中特征被消除的次序即为特征的排序。
2.3 基于随机森林的基尼不纯度指标和平均精确度指标随机森林提供了两种特征选择的方法[14]：平均不纯度减少和平均精确度减少。基于随机森林的平均不纯度表示每个特征对误差的平均减少程度，而基于随机森林的平均精确度则表示特征的特征值顺序变动对模型的精确度的影响。对于不重要的特征而言，特征的特征值顺序的变化对模型的精确度的影响不会太大，而对于重要的特征来说，该变化则会降低模型的精确度。因此，本文亦采用上述两个指标对特征进行选择。
2.4 随机森林随机森林最早由Breiman[15] 、刘坚[16]等提出，是一种以多棵决策树作为分类器对研究样本开展训练和预测的模型。其基本原理是通过自助重采样技术（Bootstrap），从原始训练样本集中有放回的重复随机抽取一定的有样本数生成新的训练样本集，然后根据选取的新训练样本数生成多个完全独立的决策树分类器，将这些分类器组合在一起就形成了随机森林模型。对预测数据而言，分类结果要根据这些决策树分类器最终的投票多少确定，其实质属于决策树模型的一种改进算法[17]。
-
3 数据分析
3.1 评价单元滑坡单元的确定是易发性评价的第一步，其划分的合理性直接关系到后期计算数据量的大小和计算模型的适用性，此次评价单元的划分在综合考虑滑坡的规模和地形图比例尺这两个因素的基础上确定。根据研究区滑坡地质灾害调查资料，区内滑坡长度和宽度主要集中在30 m以内，约占总数的85%，因而可以将区内滑坡抽象为以30×30 m划分的栅格的一个像素，因此此次研究利用ArcGIS将地形图内插成30×30 m的DEM。所有影响因子图层均转换为像元为30 m大小的栅格图层。
3.2 评价指标选取滑坡致灾因子最为复杂多样，因此滑坡预测成为各种地质灾害预测的重点和难点，科学合理的选择其致灾因子是滑坡预测的关键。结合研究区自然地理特征、滑坡灾害分布特征以及已收集滑坡灾害有关的各类数据的可获取性和精度，在参阅以往研究的基础上[18-20]，本文初步选取高程、坡向、坡度、坡位、微地貌、剖面曲率、平面曲率、地形湿度指数、岩性、距断层距离、植被覆盖率、距河流的距离、多年汛期平均降雨、土地利用类型和距道路的距离等15个致灾因子作为研究区滑坡灾害易发性评价因子。
3.3 评价指标分析（1）高程：高程因子与滑坡的发育之间在物理意义上无直接的关系，但是，由于土壤类型、植被类型和人类工程活动等与高程分带密切相关[21]，所以该因子经常被视为滑坡易发性评价的重要因子[22-24]。本研究把研究区的高程分为8级，依次为<136 m、 136~249 m、 249~366 m、 366~489 m、489~631 m、 631~821 m、 821~1078 m、>1078 m。通过高程与灾害点叠加图可知（图2（a）），滑坡密度总体上与高程呈负相关关系。
（2）坡向：坡向对于滑坡的影响，主要体现在不同的坡向，其风强、阳光等自然条件不同，从而影响了斜坡表面的植被覆盖、表面水的蒸发和下渗以及表面的风化作用等。本研究将坡向划分为平面和8个方向，8个方向为北（337.5°~360°，0~22.5°）、西北（292.5°~337.5°）、西（247.5°~292.50°）、西南（202.5°~247.5°）、南（157.5°~202.5°）、东南（112.5°~157.5°）、东（67.5°~112.5°）、东北（22.5°~67.5°）。通过坡向与灾害点叠加图可知（图2 （b）），各个坡向上滑坡密度：平面<东北<北<东<西南<南、东南<南西、西北，除了东北，其余坡向区域历史滑坡密度相差不大，西北方向滑坡密度最大为0.077个/km2。
（3）坡度：本研究基于DEM模型，通过自然间断点分级法，将研究区坡度划分为8个等级，分别为>60°、 50°~60°、 40°~50°、 30°~40°、 20°~30°、10°~20°、5°~10°、<5°。通过坡度与灾害点叠加图可知（图2（c）），坡度5°~10°的区域的历史滑坡密度最高，为0.081个/km2，这与该区域受人为活动影响较大相关。
（4）坡位：本研究利用ArcGIS Topography Tools中的坡位指数模块，依据坡位划分标准[25]，得到研究区坡位与灾害点叠加图（图2（d））。从图中可以发现，谷底和平坡的滑坡密度最大，分别为0.076个/km2、0.082个/km2，这主要由于这两个坡位区域是人类活动最为强烈的地区。
（5）微地貌：微地貌对滑坡的影响主要是通过影响植被类型、地表径流、地下水水位以及地下水分布等而实现。根据微地貌划分标准[25]，此次利用ArcGIS Topography Tools中的微地貌指数模块提取微地貌指标，生成微地貌与灾害点叠加图（图2 （e））。从图中可以看出，U型山谷、峡谷和空旷斜坡处的滑坡密度最大，达到0.089、0.082和0.082个/km2；平原中的小山次之，为0.062个/km2。其中空旷斜坡处滑坡密度高的原因是因为该微地貌处为人类活动频繁区域，且松散堆积物较多，有利于滑坡形成。
（6）剖面曲率：本研究基于DEM模型，通过自然间断点分级法，以0.5作为一个分级区段，将研究区剖面曲率划分为8级，分别为>1.5、 1~1.5、0.5~1、 0~0.5、-0.5~0、-1~-0.5、-1.5~-1、<-1.5。由研究区剖面曲率与灾害点叠加图可知（图2 （f）），滑坡密度在-0.5～1剖面曲率区间处较高，为0.058个/km2以上，说明大部分滑坡集中在较为平缓的凹入或凸起区域，这是因为这些区域人类活动强烈、松散堆积物质较多。
（7）平面曲率：本研究基于DEM模型，通过自然间断点分级法，将研究区平面曲率划分为8级，分别为<-1.5、-1.5~-1、-1~-0.5、-0.5~0、0~0.5、0.5~1、1~1.5、>1.5。由平面曲率与灾害点叠加图可知（图2（g）），滑坡密度整体上与平面曲率呈负相关关系，主要集中在较为平缓的凹入区域，在-1.5～-1的地方滑坡密度最大，达0.076个/km2，这是因为这些区域人类活动强烈、松散堆积物质较多。
（8）地形湿度指数：地形湿度指数（TWI）被广泛应用于地貌、土壤和水文等领域，是评价土壤水分空间分布的复合地形指数，其公式为：
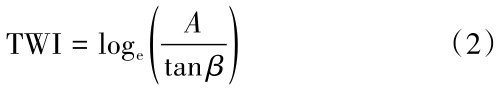
式（2）中，A为汇流累积量（m2）； β为局地坡度（°）。
此次研究利用ArcGIS中的水文分析模块，根据TWI公式，对研究区地形湿度指数进行计算，并通过自然间断点分级法，将其分为8级，分别为>20、14~20、12~14、10~12、8~10、6~8、4~6、<4。由地形湿度指数与灾害点叠加图可知（图2 （h）），滑坡密度在14～20地形湿度指数区间的数值最大，达0.218个/km2。
（9）地层岩性：本研究将岩性相似的归为一类，总共将研究区地层分为8类。由地层岩性与灾害点叠加图可知（图2（i）），不同岩性对滑坡的影响大不相同。
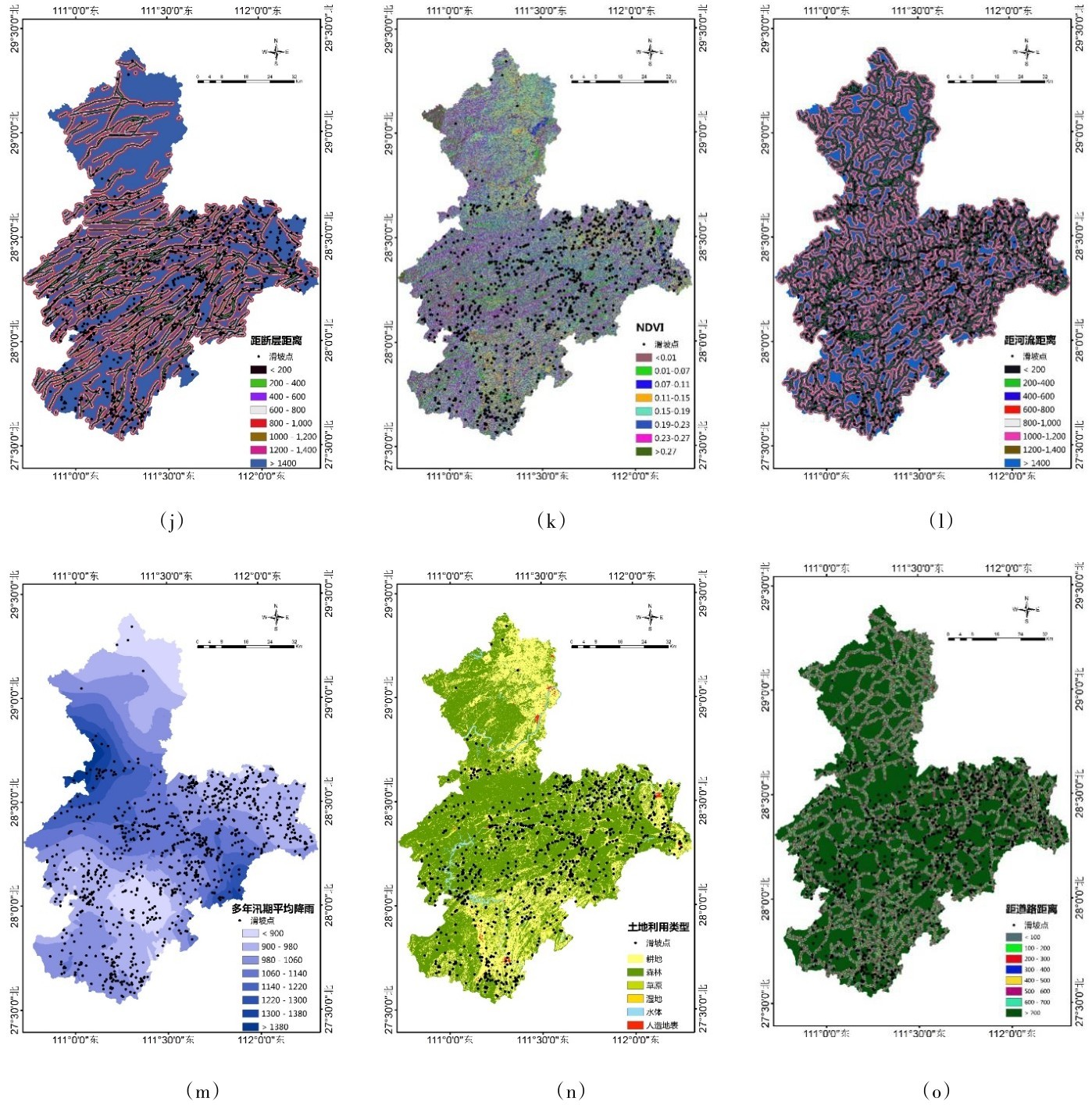
（10）距断层距离：本研究将研究区断层数据进行8个等级的多重缓冲，分别为<200 m、200~400 m、 400~600 m、 600~800 m、 800~1000 m、1000~1200 m、1200~1400 m、>1400 m。由断层距离与灾害点叠加图可知（图2（j）），距断层距离和滑坡密度有明显的统计关系，随着距断层距离的增加滑坡密度逐渐减少。
（11）植被覆盖率：本研究的NDVI数据利用landsat8OLI数据（30 m分辨率）通过计算得到，并对NDVI数据进行了重分类，将其分为8个等级，依次为<0.01、 0.01~0.07、 0.07~0.11、 0.11~0.15、0.15~0.19、 0.19~0.23、 0.23~0.27、>0.27。由植被覆盖率与灾害点叠加图可知（图2（k）），总体上滑坡密度与NDVI呈负相关关系，主要原因是NDVI高值区的植被覆盖度高，植被固坡能力较高，不易发生滑坡。
（12）距河流的距离：通过对河流数据进行缓冲操作，建立8个等级的缓冲区，分别为<200 m、200~400 m、 400~600 m、 600~800 m、 800-1000 m、 1000~1200 m、 1200~1400 m、>1400 m。由河流与灾害点叠加图可知（图2（l）），随着距河流距离的增加，滑坡密度逐渐降低。距离河流在<200 m区域的滑坡密度高达0.117个/km2，可能是由于这些区域受到河流较大的影响同时，还因河流两岸人类工程活动相对集中，从而破坏了斜坡的稳定性，导致滑坡的发生。
（13）多年汛期平均降雨：本次研究中选取的是2015—2018年共四年的汛期平均降雨量，使用ArcGIS软件对研究区的降雨图层进行重分类，分为 5 级，依次为<900， 900～980， 980～1060， 1060～1140， 1140～1220， 1220～1300， 1300～1380，>1380。由平均降雨量与灾害点叠加图可知（图2（m）），滑坡密度随多年平均降雨量的增加先增加后减少，特别是在900-980处滑坡密度最大，达到0.089个/km2。
（14）土地利用类型：本研究利用第三次土地调查成果，结合区内滑坡分布特征，制作了土地类型与灾害点叠加图（图2（n））。由图可知，人造地表的滑坡密度最大，高达0.178个/km2，耕地的滑坡密度在第二位，达到0.106个/km2，这是因为这两个土地类型均与人类活动密切相关[26]；林地、草地的滑坡密度很小，因为林地植被覆盖度很高，降水时可以有效的缓解地表降水的强度，同时植被的根系的固坡能力较大，能有效降低滑坡发生概率。
（15）距道路的距离：本研究对道路进行不同等级的缓冲区分析，将道路距离分为8级，分别为<100 m、 100~200 m、 200~300 m、 300~400 m、400~500 m、500~600 m、600~700 m、>700 m，从道路距离与灾害点叠加图可知（图2（o）），随着距道路的距离的增加，滑坡密度逐渐减小，二者呈明显的负相关关系。
3.4 评价指标优化为了从众多特征中求出那些对分类识别最有效的特征，从而实现特征空间维数的压缩，获取一组“少而精”且分类错误概率小的分类待征。本次研究利用最大互信息系数、递归特征选择、
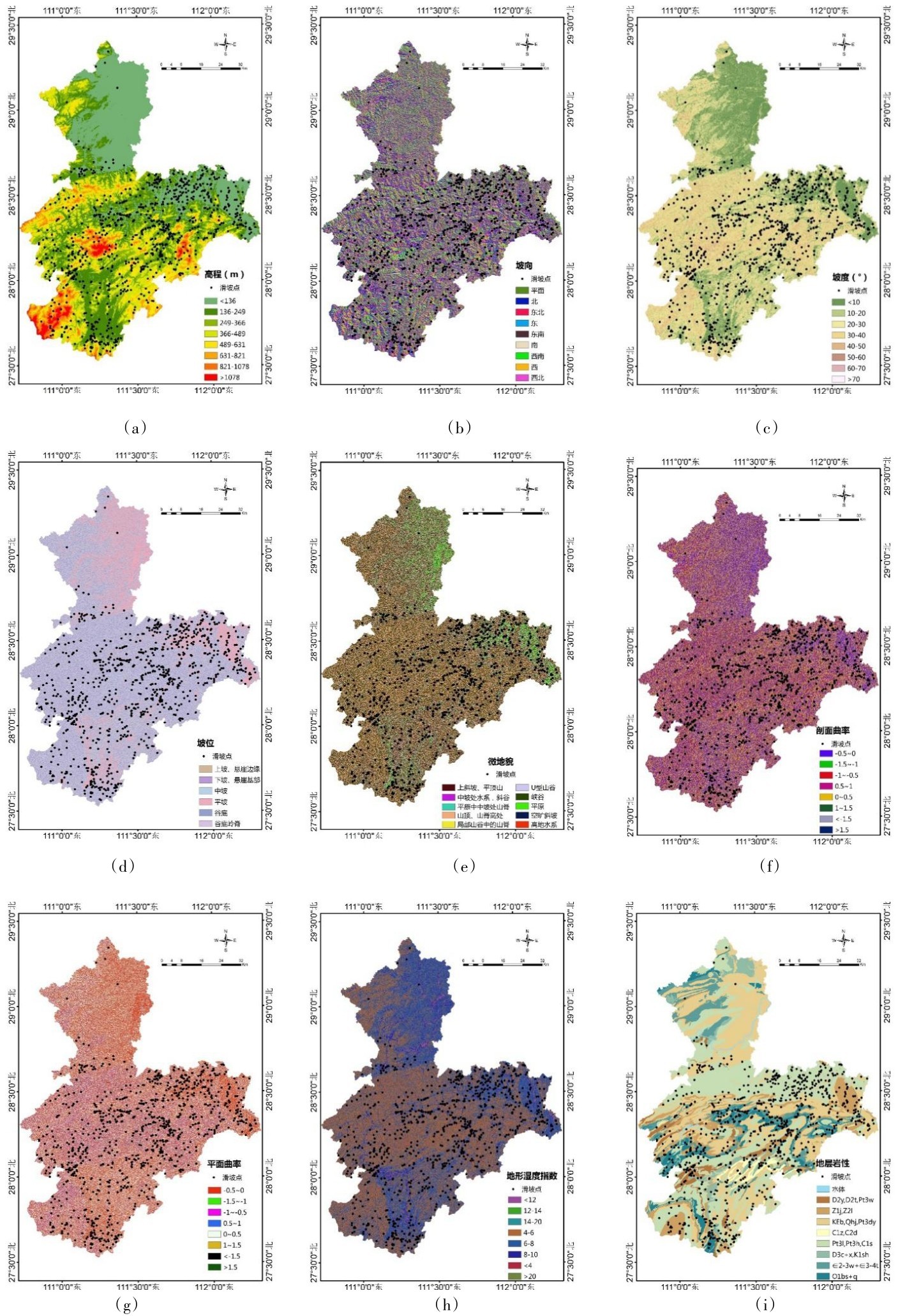
图2 滑坡影响因子与滑坡点叠加图Fig.2 Position relationship between the landslide points and the landslide influence factors
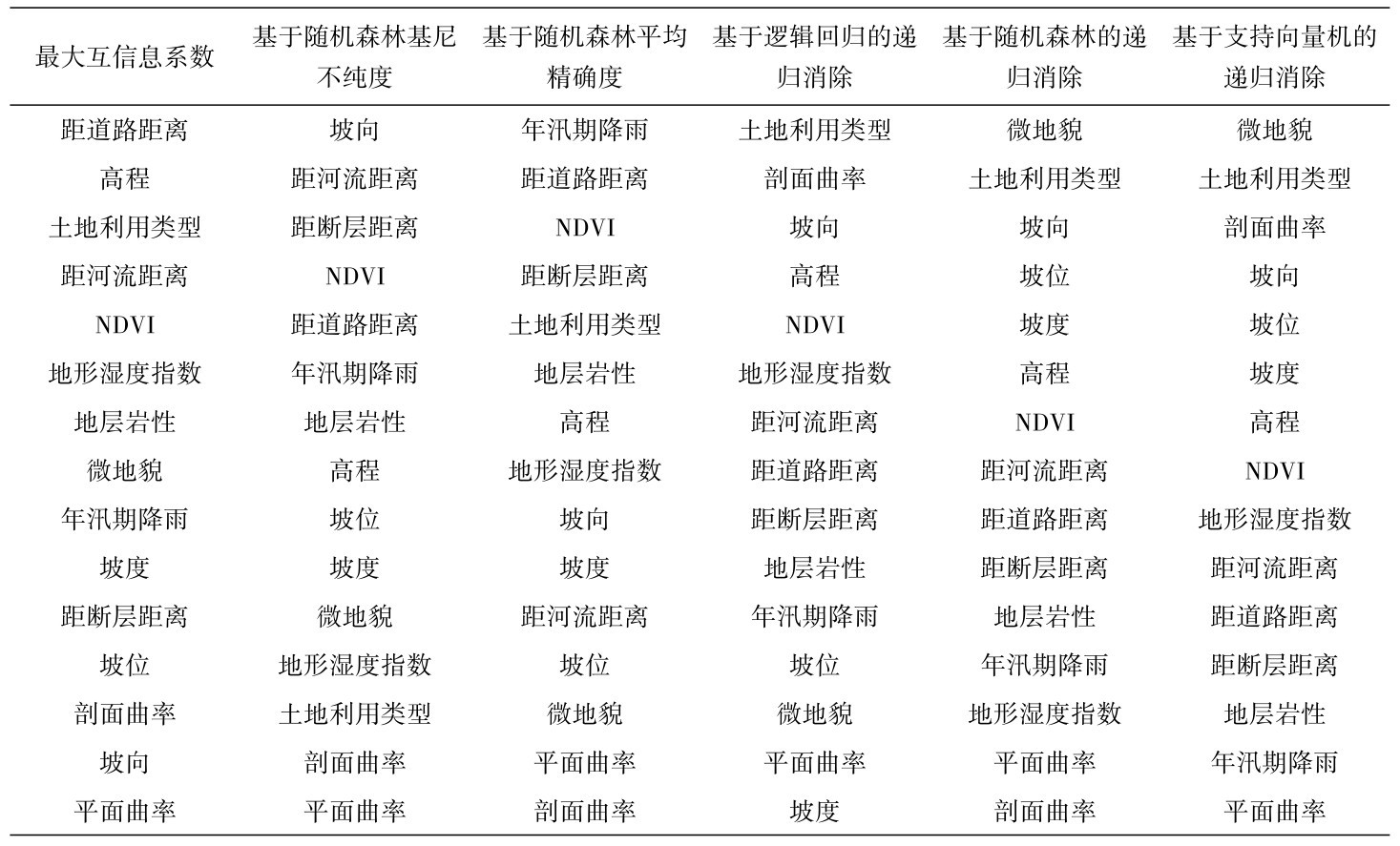
基于随机森林的基尼不纯度指标和平均精确度指标等方法进行了特征选择（表1）。
由表1的排序可以看出多种特征选择方法都将平面曲率和剖面曲率作为不重要的因子进行处理，其次是微地貌与坡位。土地利用类型、距道路的距离被各种方法一致识别为几个最重要的因子，这可能是因为在居民点、交通线路、梯田、矿区、毁林、荒地等区域内或附近，人类工程活动较为频繁，存在较多的滑坡，导致特征选择结果倾向于选择土地利用类型、距道路的距离等与工程活动有关系的因子，认为其对滑坡的发生与否影响较大。实际调查结果也显示研究区内滑坡主要由降雨和人类工程活动诱发导致，从而证实了上述特征选择方法的合理性。
基于以上特征选择结果，本次研究最终选取年汛期降雨、距道路距离、NDVI、距断层距离、土地利用类型、地层岩性、高程、地形湿度指数、坡向、坡度、距河流距离、坡位、微地貌等13个因子作为评价指标。
-
4 易发性评价
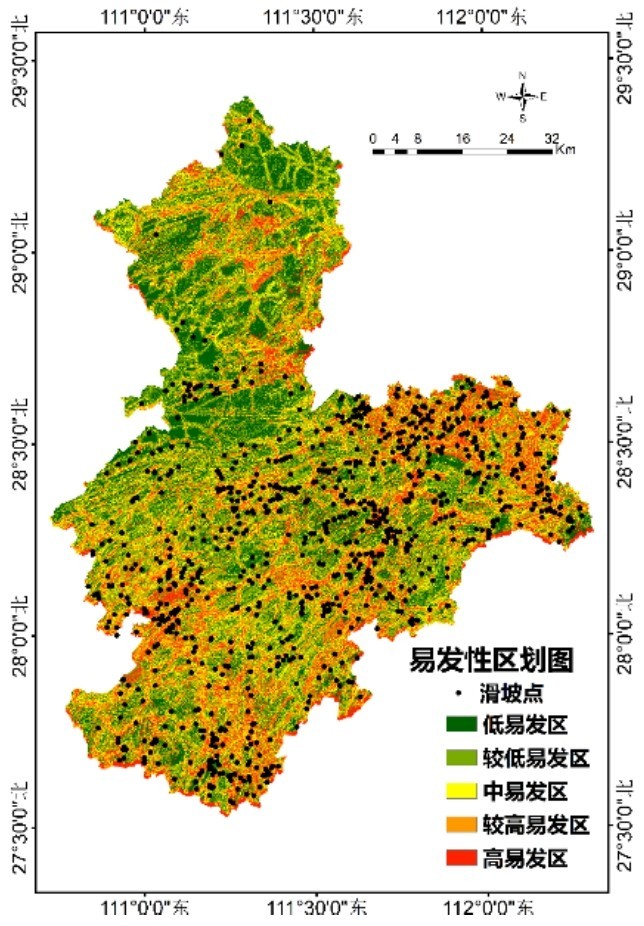
4.1 易发性评价结果根据评价指标优化结果，利用随机森林模型，再依据自然断点法划分易发性等级，沿袭前者的研究[27-29]，将易发性等级划分为5级，做出的最终区划结果图如图3和表2所示。
表1 六种特征选择方法产生的15个因子的重要性降序排列表Table 1 The descending order of importance of 15 factors generated by six feature selection methods
图3 滑坡灾害易发性分区图Fig.3 Zoning map of landslide disaster susceptibility
由表2可知，该模型中易发区、较高易发区、高易发区滑坡密度分别为0.068个/km2、0.093个/km2和0.15个/km2，滑坡灾害点在中易发区、较高易发区、高易发区分布个数占比累计为77.58%，占比较高。
4.2 结果验证为了验证模型的准确性，此次研究利用ArcGIS将研究区内2021—2022年最新滑坡点位数据与滑坡易发性区划图进行叠加分析和数理统计（表3）。由表3可以看出最新的滑坡灾害点在中易发区、较高易发区与高易发区占比分别为23.04%、29.57%和26.97%，累计占比79.58%，占比较高，说明研究区域的滑坡易发性区划图划分的较为成功。
表2 滑坡灾害点易发性分布表Table 2 Statistics of susceptibility of the landslide disaster points
表3 2021—2022年滑坡灾害点易发性分布表Table 3 Statistics of susceptibility of the landslide disaster points from 2021 to 2022
-
5 结论
本研究利用最大互信息系数、递归特征选择、基于随机森林的基尼不纯度指标和平均精确度指标等方法对湖南中西部地区滑坡影响因子进行了优化，然后利用随机森林方法对研究区滑坡易发性进行了研究，通过易发性评价结果和最新滑坡数据对比得到以下结论：
（1）多种方法对比优选滑坡影响因子，随机森林算法进行滑坡易发性评价，结果验证显示该方法准确度高、实用性强；
（2）平面曲率和剖面曲率对湖南省中西部滑坡的影响较小，降雨和人类工程活动是区内滑坡的主要影响因素；
（3）研究区高易发区和较高易发区整体呈带状分布，与人类聚集区重叠性较好，表明人类活动是致使滑坡发生的关键因素，今后研究工作应进一步加强人类活动对滑坡影响的细化和定量评价。
- [1] Neuland， Herbert. A prediction model of landslips[J]. Catena，1976，3（2），215-230
- [2] Rasmussen C E，Nickisch H. Gaussian processes for machine learning （GPML）toolbox[J]. Journal of Machine Learning Research，2010，11（6），3011-3015
- [3] Chen Weitao，Li Xianju，Wang Yanxin，et al. Forested landslide detection using LiDAR data and the random forest algorithm： a case study of the Three Gorges， China[J]. Remote Sensing of Environment，2014（152）：291-301.
- [4] Amiri M，Pourghasemi H R，Ghanbarian G A，et al. Assessment of the importance of gully erosion effective factors using Boruta algorithm and its spatial modeling and mapping using three machine learning algorithms[J]. Geoderma，2019（340）：55-69.
- [5] Abu El-magd S A，Ali S A，Pham Q B. Spatial modeling and susceptibility zonation of landslides using random forest， naïve bayes and K-nearest neighbor in a complicated terrain [J]. Earth Science Informatics，2021，14（3）：1227-1243.
- [6] Van Den Eeckhaut M，Marre A，Poesen J. Comparison of two landslide susceptibility assessments in the Champagne-Ardenne region（France）[J]. Geomorphology，2010，115（1/2）：141-155.
- [7] Zhou C，Yin K L，Cao Y，et al. Landslide susceptibility modeling applying machine learning methods：a case study from Longju in the Three Gorges Reservoir area，China[J]. Computers&Geosciences，2008（112）：23-37.
- [8]付旭东，王金艳，李龙燕，等.基于随机森林算法的风场预报[J].兰州大学学报（自然科学版），2021，57（4）：503-509.
- [9] Sajadi P，Sang Y F，Gholamnia M，et al. Evaluation of the landslide susceptibility and its spatial difference in the whole Qinghai-Tibetan Plateau region by five learning algorithms [J]. Geoscience Letters，2022（9）：1-25.
- [10] Sun D L，Gu Q Y，Wen H J，et al. A hybrid landslide warning model coupling susceptibility zoning and preci-pitation[J]. Forests，2022，13（6）：827.
- [11]郭明珠，刘晃，王欢欢，等.金沙江上游贡扎村岩质滑坡发育特征及演化成因分析[J].地震研究，2021，44（2）：242-250.
- [12] Reshef D N，Reshef Y A，Finucane H K，et al. Detecting novel associations in large data sets[J]. Science，2011，334 （6062）：1518-1524.
- [13] Guyon I，Weston J，Barnhill S，et al. Gene selection for cancer classification using support vector machines[J]. Machine learning，2022，46（1-3）：389-422.
- [14]姚登举，杨静，詹晓娟.基于随机森林的特征选择算法[J].吉林大学学报（工学版），2014，44（1）：137-141.
- [15] Breiman L. Random forests[J]. Machine Learning，2001，45 （1）：5-32.
- [16]刘坚，李树林，陈涛.基于优化随机森林模型的滑坡易发性评价[J].武汉大学学报（信息科学版），2018，43（07）：1085-1091.
- [17]姚雄，余坤勇，刘健，等.基于随机森林模型的降水诱发山体滑坡空间预测技术[J].福建农林大学学报（自然科学版），2016，45（02）：219-227.
- [18] Wang L Q，Zhang Z H，Huang B L，et al. Triggering mechanism and possible evolution process of the ancient Qingshi landslide in the Three Gorges Reservoir[J]. Geomatics Natural Hazards & Risk，2021，12（1）：3160-74.
- [19] Zhang K Q，Wang L Q，Zhang W G，et al. Formation and failure mechanism of the Xinfangzi landslide in Chongqing City（China）[J]. Applied Sciences，2021，11（19）：8693
- [20]白仙富，戴雨芡，叶燎原，等.基于GIS和专家知识的滇西南地区滑坡敏感性模糊逻辑推理方法[J].地震研究， 2022，45（1）：118-131.
- [21] Li L，Lan H，Guo C，et al. A modified frequency ratio method for landslide susceptibility assessment[J]. Landsli-des，2016，14（2）：727-741.
- [22] Long J J，Liu Y，Li C D，et al. A novel model for regional susceptibility mapping of rainfall reservoir induced landslides in Jurassic slide-prone strata of western Hubei Province， Three Gorges Reservoir area[J]. Stochastic Environmental Research and Risk Assessment，2021，35 （7）：1403-26.
- [23] Sun D L，Xu J H，Wen H J，et al. Assessment of landslide susceptibility mapping based on Bayesian hyperparameter optimization：a comparison between logistic regression and random forest[J]. Engineering Geology，2021（281）：105792.
- [24] Zhou X Z，Wen H J，Li Z W，et al. An interpretable model for the susceptibility of rainfall-induced shallow landslides based on shap and xgboost[J]. Geocarto International，2022， 37（23）：1-27.
- [25] Weiss A. Topographic position and landforms analysis[R]. San Diego，CA ：ESRI user conference，2001.
- [26]叶润青，李士垚，郭飞，等.基于RS和GIS的三峡库区滑坡易发程度与土地利用变化的关系研究[J].工程地质学报，2021，29（03）：724-33.
- [27] Gariano S L，Rianna G，Petrucci O，et al. Assessing future changes in the occurrence of rainfall-induced landslides at a regional scale[J]. Sci Total Environ，2017（596/597）：417-426 .
- [28] He Q，Shahabi H，Shirzadi A， et al. Landslide spatial modelling using novel bivariate statistical based Naive Bayes，RBF Classifier，and RBF Network machine learning algorithm[J]. Sci Total Environ，2019（663）：1-15.
- [29] Juliev M，Mergili M，Mondal I，et al. Comparative analysis of statistical methods for landslide susceptibility mapping in the Bostanlik District， Uzbekistan[J]. Sci Total Environ， 2019（653）：801-814.
