双层模块装配式组合剪力墙试件由预制完成的单个剪力墙模块通过高强螺栓连接组成，如图1所示。每个模块主要由焊有外伸板的连接件与焊有栓钉的内藏钢板焊接组成钢构件，钢构件再与现浇混凝土板组合完成单个模块的预制后，再用高强螺栓将两个剪力墙模块连接形成单层组合剪力墙。等两单层组合剪力墙安装完成后，再用高强螺栓将其与上下钢梁相连，最后形成一双层模块装配式组合剪力墙。剪力墙模块平面尺寸900×450 mm，内藏钢板880×430 mm，外挂混凝土板880×430 mm，钢板厚4 mm、Q235B型钢，混凝土板厚50 mm、C40；模块之间采用8.8级M16螺栓连接，螺栓间距100 mm。

混凝土应力-应变关系采用塑性损伤模型，即文献Popovics S^[12]和Yip W K^[13]提出本构公式，可以很好模拟低围压时，混凝土受到的单调、循坏或者动载作用下的力学行为，如图2所示。混凝土本构计算公式：

图1 三维组装示意图Fig.1 Three dimensional assembly diagram

图2 混凝土应力-应变本构关系Fig.2 Stress-strain constitutive relation of concrete

式（1）、（2）中：σ'cu为混凝土的极限抗压强度；σ_c为混凝土压应力；ε_c为混凝土压应变；m为曲线拟合参数， m=0.8 + σ'cu/17； E_c为初始切线模量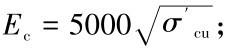， ε ₀为σ'cu作用下的混凝土压应变；K由下式可得：

混凝土拉伸应力-应变关系采用Stramandinoli R S B^[14]给出的本构关系：

α=0.017 + 0.255 ( nρ )-0.106 ( nρ )² + 0.016 ( nρ )³ （5）

式（3）中：f_ct为混凝土极限抗拉强度；ε_cr为f_ct对应的拉伸应变；σ_ct为混凝土拉应力；ε为混凝土拉应变；α为指数衰减参数；n=E_s/E_c，E_s为钢材弹性模量；ρ为混凝土配筋率。

混凝土损伤塑性模型可以通过损伤参数来定义混凝土在循环荷载下引起的刚度退化和刚度恢复效应，避免软化段的复杂处理。假定混凝土材料主要存在两种主要破坏：拉伸开裂和压缩破碎，这两种主要破坏引起的弹性模量变化可以采用损伤因子d（拉压损伤因子分别为d_t和d_c）描述，当d_t=0时，表示混凝土还没有发生拉伸损伤，此时混凝土拉伸刚度未退化；当d_t=1时，表示混凝土将完全拉伸破坏，此时混凝土拉伸刚度为0；当d_c=0时，表示混凝土还没有发生压缩损伤，此时混凝土压缩刚度未退化；当d_c=1时，表示混凝土将完全受压破坏，此时混凝土压缩刚度为0；具体计算公式如下：

E=(1 - d)E_c（6）

(1 - d )=(1 - s_td_c)(1 - s_cd_t)（7）

式（6）、（7）中：s_t、s_c分别为与应力反向时刚度恢复的应力状态有关参数，可以用以下方程式定义：

式（8）~（10）中：权重因子h_t和h_c控制着反向加载时混凝土材料刚度的恢复。混凝土的试验结果表明，当荷载由拉伸变为压缩时，只要裂纹闭合就可使压缩刚度得到恢复，即h_t=0；另一方面一旦出现压碎微裂纹，当荷载由压缩变为拉伸时，拉伸刚度将不能恢复，即h_c=0。

对于理想弹塑性模型，根据钢材力学性能试验，确定钢材的本构关系。以Mises折算应力作为钢材屈服的判断依据，Mises折算应力按式（11）计算：

式（11）中：σ_m为Mises折算应力；σ₁、σ₁、σ₁分别为计算Mises折算应力处材料的第一主应力、第二主应力和第三主应力。

对于钢材损伤本构模型采用文献[15]给出的应力三轴度起始损伤准则模型。假设钢材中的等效塑性应变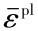 累计达到发生起始损伤的等效塑性应变 时，钢材内部发生损伤。为了减少确定钢材损伤路径的难度，且能适合钢材损伤的应用，Yu HL等^[16]建议将Lee和Wierbicki在文献[17]中的等效塑性损伤应 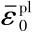与应力三轴度η路径简化表示为下式的形式：

式（1 2）中： C₁为钢材平板纯剪切状态下（η=0）的等效塑性损伤应变ε^-shear0 ； C₂为钢材开口圆棒单轴拉伸时（η=η₀）的等效塑性损伤应变ε^-axi0 ； η₀为一常数。C₂可以通过轴对称拉伸试件断裂后的截面缩小面积A_R来确定：

图3 简化后钢材应力三轴度与等效塑性损伤应变路径Fig.3 Stress triaxiality and equivalent plastic damage strain path of simplified steel Stress

C₂ =-ln (1 - A_R)

另外C₁与C₂又可通过式（13）、（14）进行换算：

式（13）、（14）中：K、n为钢材硬化参数，在钢材拉伸试验的真实应力-应变曲线上取屈服应力到极限应力段可通过式（9）拟合算出K、n。函数关系来表示。

内藏钢板和连接件、内藏钢板和栓钉以及连接件和外伸板间的连接在实际现场施工中皆使用焊接方式，故在模拟中用绑定“Tie”约束模拟；栓钉与现浇混凝土之间的作用采用嵌入方式来模拟；钢构件与两侧混凝土板的接触法向方向采用“硬接触”，切向采用库伦摩擦，摩擦系数为0.25。对高强螺栓施加相应预应力，且高强螺栓与外伸板间相接部分采用有摩擦的“硬”接触。型钢和混凝土材料均采用8节点六面体线性减缩积分三维实体单元C3D8R模拟。采用结构化网格划分方法对部件进行网格划分。

如图3所示，钢材在不同应力三轴度区段内分别发生剪切损伤（-1/3≤η≤0）、复合损伤（0≤η≤η₀）与延性孔洞扩展损伤（η≥η₀）三种损伤形式，分别对应钢材在压缩、剪拉与拉伸状态时损伤的情况。当钢材承受的等效塑性应变在曲线下方时，钢材不发生损伤；反之，当钢材的等效塑性应变超过曲线，则进入损伤状态。此时钢材峰值应力后的下降路径可以表示为式（16）中剩余应力的形式。在应力下降的区段内，钢材的剩余模量与剩余应力之间的关系可由标量D来表示：

底部框架梁采用固结约束形式，即约束6个自由度。为模拟上部加载梁往复运动，在有限元模型中限制加载梁除了加载方向外的其他方向的运动，并设置一个参考点，将加载梁上所以节点的所有自由度与参考点耦合，再通过参考点对构件进行力和位移加载，如图4所示。参考点仅有沿加载梁梁长方向的运动，其他方向的位移均为零。图5为加载制度示意图。

式（15）、（16）中：E、σ为钢材的弹性模量与屈服应力 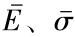为钢材应力下降段内的剩余模量与剩余应力；D定义为钢材的损伤因子，取值范围在[0，1]之间。因损伤因子应表示为钢材等效塑性应变的函数，考虑到在有限元模拟中单元 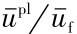，将钢材损伤因子D用式（17）与塑性位移 的

为验证上述双层模块装配式组合剪力墙建模方法的合理性，采用如图6所示的单层装配式组合剪力墙的抗震性能试验研究成果^[18]，对上述有限元模型的建模方式、本构关系及边界处理加以验证。本文与该文献研究的不同之处仅在于双层与单层的区别，其余模型参数都一致，因而验证结果具有较高的可信度。

图4 有限元模型示意图Fig.4 Schematic diagram of FEM

图5 加载示意图Fig.5 Loading diagram

图7给出了试件在加载完成后，内藏钢板和外挂混凝土板的破坏图，图8为两者在数值模拟完成后的破坏图。从图8（a）和图8（b）中可以看出，试验中内藏钢板的破坏主要集中在框架的四个角部，其中底端的角部破坏最大，同时内藏钢板表面出现了明显的“拉力带”，通过对比可知，这与模拟的结构图完全吻合。从图8（c）和图8（d）中可以看出，对于外挂混凝土板，试验中在螺栓孔和角部出现破坏，模拟中混凝土板的压缩和拉伸损伤主要出现在螺栓孔和角部，两者的破坏形态基本吻合。图9给出了滞回曲线试验与有限元结果的对比图，表2为部分参数对比结果。可见，当型钢材料仅采用弹塑性强化本构时，模型随着加载位移的增加，其承载能力一直在增加，与试验结果难以吻合。当型钢材料采用塑性损伤本构时，模拟滞回曲线与试验结果具有很好的一致性：弹性阶段随位移角的增加承载力也随之增加，型钢进入屈服后承载力增长放缓，钢材开始进入损伤状态，最后因钢板损伤过大而造成承载力不断下降。试验与数值模拟结果屈服荷载、峰值承载力、初始刚度的误差分别为6.23%、 1.05%、 5.40%，虽然存在一定的差异，但从对比结果来看，其精确度已能满足工程要求，说明所采用的建模方式和考虑塑性损伤本构关系能较好地反映组合剪力墙试件的真实受力性能，可为后续双层模块化装配式组合剪力墙的参数分析提供支撑。

图6 单层装配式组合剪力墙Fig.6 Single-layer fabricated composite shear wall

图7 试件破坏图ig.7 Diagram of specimen failure

图8 试件破坏图Fig.8 Diagram of specimen failure

图9 滞回曲线对比图Fig.9 Comparison diagram of hysteretic curve

为探究该双层模块装配式组合剪力墙的抗震性能，通过改变基本模型的跨高比、高厚比、混凝土板强度和栓钉间距4个变量，并基于上述所建立的双层组合剪力墙的有限元模型为基本模型（S2）与传统普通剪力墙（S16）进行对比（见表2），分析不同因素对该剪力墙抗震性能的影响，具体工况见表3。

表2 试验与有限元模拟结果对比Table 2 Comparison of test and simulation results

表3 分析工况表Table 3 Condition table