1.1 本征时间尺度分解法算法(ITD)
设Xt为待处理离散信号,并将L定义为基线提取算子,定义Xt=LXt+(1-L)Xt=Lt+Ht,则离散信号的均值曲线表示为LXt,简单记录为Lt,将Ht=(1-L)Xt定义为合理旋转分量(PR),ITD 算法具体分解流程如下:
(1)确定信号Xt(t≥0)的极值点Xk及对应的时刻τk(k=1,2,3,…,N,N 为所有极值点的个数),简单起见定义τk=0。另假设Lt和Ht定义在区间(0,τk),Xt满足区间范围t∈(0,τk+2)。然后定义信号的分段线性基线提取因子L在t∈(τk,τk+1)范围内为:

其中t∈(τk,τk+1);a为控制提取固有旋转分量幅度的增益控制参数,0<α<1,通常取α=0.5。
(2)定义合理旋转分量提取因子H,利用计算得到的基线分量Lt可得PR分量Ht为:
Ht=HXt=(1-L)Xt=Xt- Lt (3)
(3)将Lt作为下一次分解的输入信号,采用上述步骤进行再次分解,直至最终基线分量单调,则分解过程终止。
(4)通过多次ITD分解,待处理离散信号分解为若干合理旋转分量(PR)和一个单调趋势项之和,最终分解结果可以表示为:
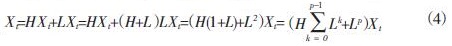
其中HLkXt为第k+1阶的合理旋转分量,LPXt为单调趋势项或最低频率基线。
从上述算法分析,ITD方法中基线的定义是基于信号的线性变换避开了EMD中使用两次三次样条拟合,因此可以减少计算时间,降低拟合之后的误差,所以ITD方法适合在线实时的处理数据。
1.2 基于ITD 的强震动加速度数据处理流程
将原始加速度记录通过本征时间尺度分解法算法(ITD)分解后,从原始加速度记录中去除分解后的趋势项,然后通过设计的带通滤波器即可得到校正后的加速度记录,然后通过梯形积分法积分得到速度和位移结果,通过统计分析可以得到最大加速度(PGA)、速度(PGV)和位移(PGD),进一步将校正后的加速度进行变换可以得到傅里叶谱和反应谱等信息,该处理方法具有简单、高效的特点,具体数据处理流程如图1所示。
图1 基于ITD 的强震动数据处理流程
Fig.1 The strong vibration data processing flow based on ITD method