1.1 基于贡献率法的地形地貌因子计算
贡献率是经济统计学分析中关键方法,将其引入到地质灾害分析中,可以分析各个地形地貌因子在地震后的状态,并对其进行量化处理,为后续敏感性评价作理论基础。在分析地震后地质变化过程中,把贡献率引入各个地貌因子内,对发生改变的程度进行量化处理。
滑坡发生趋势取决于敏感性程度,而敏感性高低在于地震后地形地貌发生的改变。想要评价某区域滑坡灾害性的大小,就需考虑区域内存在的地形地貌因子的量化数值,地貌影响因子可以划分成一级与二级两个等级,分别记为频率因子的面积因子。用fij和aij来描述:
详细贡献率量化过程如下:
wij=f(fij,aij) (1)
其中,w描述的是地貌因子贡献率,fij描述的是第i个频率因子和第j个面积因子频率之和。式(1)就能够描述为不同级影响因子中任意范围内的地质变化次数以及全部系数和的比值。aij描述第i个和因子变化数量之和的比值。aij描述第i个和因子当中j个二级因子总面积因子。
滑坡面积总和的两数相比所得值,通过与二级因子中每类因子区域范围内的滑坡面积之和,可分析贡献率的指标大小计算如下:
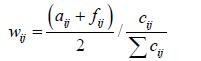 (2)
(2)
随后进行归一化处理,得到式(3)
 (3)
(3)
式中cij表示第j个二级因子所对应的区域面积值。
1.2 确定性系数下敏感性分析
确定性系数CF方法(Certainty Factor Merhod)是由Shorliffe和Buchanan提出的一个概率函数,并且由Heclerman进行完善改进,将此用来分析某种事件发生过程当中各个影响因子的敏感性。此方法在评估不同种类灾害影响因子敏感性有很高的精准度。CF方法表示如下:
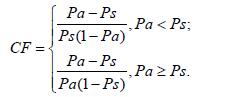 (7)
(7)
式(7)中, Pa为事件在数据类 中发生的条件概率。在现实地震滑坡影响因子敏感性分析中,Pa可以表示数据类a的中已经有滑坡面积与此数据类单元面积的比值,Ps可以表示为区域内的地震滑坡面积与区面积的比值。CF的变化区间为[-1,1],当CF>0时,CF值越大,表示坡体变形程度越高,发生滑动的可能性越大;相反CF<0时,CF越小,表明地震诱发滑坡的可能性越小;当CF接近0时,则是表明坡体滑动的可能无法确定。
本文借助GIS工具的空间分析功能,完成每个影响因子的CF计算合并。首先将影响因子按一定原则分成不同类别,然后在AreGIS中将每个影响因子的面积和所包含的地震滑坡面积,根据式(7)计算出每类影响因子中每一个因子的CF值。由于每类影响因子包含很多子集,每个子集又包含不同的单一因子,这些单一因子的CF值可能都不相同,会导致出现敏感性程度较为分散的CF值,不利于关键影响因子类集的筛选。为了对各类因子的作用程度进行分类排序,本文利用一个统一值Z值来反映各大类影响因子整体对地震滑坡的敏感性,Z值所体现的是每一类影响因子的各子集及各单一因子CF值的总合效果,可以更为直观准确的确定区域内地震诱发滑坡发生的关键因子。Z值可以根据式(8)对各类影响集(子集)中影响因子的CF值进行合并来得到,公式表达如下:
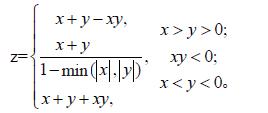 (8)
(8)
式(8)中,x和y分别表示要合并的两个CF值,因本文将从小到大对每类影响因子下各子集的CF值合并,最终得到体现该类各因子集综合作用的Z值。通过每一类Z值的比较,可以发现不同类别影响因子对地震滑坡的影响程度,从而确认主要因子的种类,每一类影响因子的Z值可以反射出区域内此类因子对地震滑坡的影响有没有普遍的性质。然后再利用CF值对各类具体影响因子进行名敏感性分析。一般情况下,Z值越大表明该影响因子在地震滑坡的形成过程中越起到关键作用,而CF值越来越大则表明对应单一影响因子敏感越高。因此,在因子确认中,可以借助Z值确认某一类因子的关键程度,利用CF值来确认某一特定因子的敏感度。因子敏感性分析流程如图1。
图1 地震滑坡确定系数分析流程
Fig.1 Analysis flow of determination coefficient of earthquake landslide min
1.3 敏感性评价
1.3.1评价体系建立
评价的基础为地质因子、外界诱发因子以及人为因子结合。在地质灾害空间分布以及地质环境特征分析的基础之上,为了突显出地形地貌的主导因子,本文利用因子容量、可图形化以及经济能力的可靠性,并结合GIS分析工具进行评价,着重摘选了地形指标、地震烈度指标参与分析研究,组成了敏感性评价体系,如图2所示。
图2 敏感性评价指标体系
Fig.2 Sensitivity evaluation index system.
1.3.2指标量化敏感性统计
敏感性计算中指标量化的过程非常重要,直接对评价结果产生重要影响。量化方法数量甚多,相比之下数学统计量化法占据较好的适用性,计算结果也相对较精准。敏感性统计是计算各类指标因子属性的地质灾害点平均密度之间整体频率,敏感性评价就是通过整体频率多少来进行判定的。
详细敏感性统计过程如下:
步骤1:依据敏感度大小程度进行敏感性等级划分。
步骤2:运用GIS计算各类标准属性的面积和单位面积中灾害点数,并且统计各类标准属性在单位面积的灾害点个数,再与地质灾害点平均密度结合比值要求对数,来表现出敏感性程度。
步骤3:分别各个图层栅格化。
步骤2的敏感性统计如下:
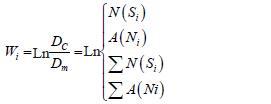 (4)
(4)
式中:wi为某一种特殊标准的敏感性;Dc为此类特殊标准的地质灾害分布密度;Dm为整区域内地质灾害分布密度;N(Si)为此类特殊标准的地质灾害点个数;∑N(Si)为地质灾害点总个数; A(Ni)为某一中特殊标准所占的总面积;∑A(Ni)为评价区的总面积。
1.3.3指标敏感权重
指标赋予地质灾害敏感性权重值,采用用层次分析法(AHP)建立评价矩阵。本文需要考虑地形坡度、岩性、海拔高度、地震烈度、距河流距离共5个评价指标,指标敏感性分析以及敏感度结果见表1所示,最后构建的评价矩阵见表2。
在Matlab下求得评价矩阵的最大征值λmax=5.0133,一次性指标CI=(λmax-n)/(5-1)=(5.0133-5)/(5-1)=0.0133/4=0.003325,找寻任意平均值已执行标准(RI);(RI=1.12),则其检验性指标CR=CI/RI=0.00277<0.1。最大特征值对应法特征向量为,对特征向量进行归一处理即得到5个评价指标的权重wi(见表2)。
表1 指标敏感性分析和敏感度赋值
Table 1 Index sensitivity analysis and sensitivity assignment
表2 指标判断矩阵和权重
Table 2 Index judgment matrix and weight
注释:B1描述为地形坡度;B2描述为海拔高度;B3描述为岩性;B4描述为地震烈度;B5描述为距河流距离;Wi描述为指标权重。
本文的敏感性评价是利用GIS空间分析模块Map calculator命令中完成的。通过以上分析计算得出:
S =∑Wi×Bij=0.157×Bij+0.088×B2j+0.156×B3j+0.297×B4j+ 0.297×B5j(5)
式中;S为评价单元的总和敏感度值;Wi为第i个指标的敏感度权重;Bij为第i个指标属性j的敏感度。其中i =1,2,3,4,5;j =1,2,3,4,5。
1.4 评价模型选择
本文采取几率数值模型、信息量评价模型对地震诱发滑坡地质灾害敏感进行评价和分析对比。
(1)几率就是某种因子类X中,存在最多因子的区域面积发生地质灾害的几率设为是100%,那么因子Xi产生地质灾害的几率由以下公式算出:
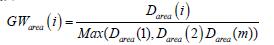 (6)
(6)
其中,GWarea(i)是因子Xi中发生地质灾害的几率,Darea(i)是因子Xi的地质灾害的面积密度。
(2)信息论是信息模型的理论基础,运用地质灾害产生时熵的减少表现出地质灾害时间所产生的不确定,地质灾害系统熵值的变化等于因子组合对地质灾害事件所带来的的不确定程度,与地质灾害的发生以及预测中得到的信息质量和数量相关,即信息量越大,所出现地质灾害的可能性越大。
I(y,x1,x2,…,xn)=log2(p(y|x2x2…xn)/Py)(7)
式(7)随后进行归一化处理,得到式
I(y,x1,x2,…,xn)=I(y,x1)+Ix1(y,x2)Ix1,x2,…xn-1(y,xn)(8)
式中I(y,x1,x2,L,xn) 描述的是具体因素组合x1,x2,… ,xn 描述的是地质灾害提供的信息量;P(y|x2 x2 … xn ) 描述的是因素x1,x2,… , xn 描述的是组合条件下地质灾害产生的几率;Py描述的是地质灾害产生的几率;Ix1,x2,L xn-1(y,x1)
描述的是因素x1,x2,… ,xn-1所存在条件下,因素xn对地质灾害所提供的信息量。
最终根据概率数值将敏感性评价为4区,分别是低敏感性区、中敏感性区、高敏感性区、极高敏感性区。