基金项目:地震监测、预测、科研三结合课题(基于广东地区强震记录的预警震级估算 CEA-JC/3JH-161902)
作者简介:杨 芳(1988- ),女,工程师,主要从事地震观测和强震监测数据分析工作。E-mail:328612609@qq.com. 通信作者:朱嘉健(1989- ),男,工程师,从事工程结构强震动监测研究。E-mail:zjjsysu@foxmail.com.
(1. 广东省地震局,广州 510070;2. 中国地震局地震监测与减灾技术重点实验室,广州 510070;3. 广东省地震预警与重大工程安全诊断重点实验室,广州 510070)
(1. Guangdong Earthquake Agency,Guangzhou 510070,China;2. Key Laboratory of Earthquake Monitoring and Disaster Mitigation Technology,Guangzhou 510070,China;3. Key Laboratory of Guangdong Province Earthquake Early Warning and Safety Diagnosis of Major Projects,Guangzhou 510070,China)
Earthquake early warning;Magnitude estimation;τc method;Moving window
DOI: 10.13512/j.hndz.2020.01.008
地震预警系统是减轻地震灾害损失的关键手段,而利用地震P波初始信息快速估算震级则是地震预警系统的重要部分。对地震预警研究中常用的基于卓越周期τc的震级估算方法进行了研究,提出了基于移动时窗的τc计算方法。研究表明:τc值会在地震波到达台站时发生显著变化,根据这种变化可更为精准地确定用于震级估计的τc值。此外,利用上述方法对广东地区的地震记录进行分析,用函数拟合该地区τc与震级的关系,建立了适用于广东地区的τc震级快速估算模型。
Earthquake early warning system is the key means to reduce the loss of earthquake disaster. The rapid magnitude estimation using the initial information of seismic P wave is an important part of earthquake early warning system. In this paper, the magnitude estimation method based on τc is studied,and a novel τc method based on moving window is proposed. The research shows that the value of τc will change significantly when the seismic wave arrives at the seismic stations. According to this phenomenon,the changes of τc can be used to estimate the seismic magnitude directly. In addition,the seismic records in Guangdong region are analyzed by utilizing the proposed method. At last, by observing the relationship between the value of τc and magnitude, a rapid magnitude estimation model is established for Guangdong area.
我国是世界上地震灾害最严重的国家之一,地震灾害本身虽然不可避免,但通过采取一些合理可行的技术手段则是能够大大减少地震引起的人员伤亡和有效减轻地震造成的财产损失。除了工程上通常采取的一些工程抗震设防措施外,地震预警技术也是能够有效减轻地震灾害的手段之一。日本新干线、中国台湾地区以及墨西哥等预警系统的多次经验证明了地震预警对防灾减灾具有不可否认的意义[1]。其中,地震震级的快速测定一直是地震预警系统中备受关注的难点,地震震级的快速自动测定无论是对地震早期预警、海啸预警等紧急地震警报的发布,还是对地震灾害的评估和判定都是具有重要的应用价值[2-4]。
近几十年来,国内外专家针对地震震级快速测定的问题开展了大量的研究。在早期的研究中,专家学者发现地震波特征周期与震级大小存在一定联系,并以此来估算地震震级。比如,Nakamura[5-7]通过计算地震波前几秒的卓越周期,最早地提出了基于P波卓越周期的τpmax 方法;随后,Kanamor[8]、Allen和Lockman等[9-11]及Olson等[12]对τpmax方法进行的深入研究,并进行了一定的改进。但他们的研究表明:τpmax方法受数据预处理过程的影响较大,得到的震级估算结果的准确性和稳定性较差。除地震波周期特征外,部分学者也研究了利用地震波数据时域及统计特征的震级估计方法,比如Ellsworth[13]和Beroza[14]认为近场P波到达后0.01~5s内存在一个幅值和震源时间函数较弱的地震成核相,可使用该现象估计矩震级大小;Greecksch 和Kümpel[15]使用统计方法对地震加速度进行分析,建立了一套基于加速度图像的震级估计方法;Wu等[16]人则研究了地震震级和地震波幅值衰减的关系,并利用该规律对震级进行估计;随着神经网络技术的发展,Leach 和Dowla[17]还使用了神经元网络方法估计不同的地面运动参数,实时预测地震动状态。
在上述震级估算方法中,基于地震P波特征周期的τc方法是利用地震波周期特性估计震级的方法之一,也是地震震级估算的有效方法之一。该方法最初由Kanamori[18]提出,是对τpmax方法的改进。基于τc方法,Wu和Kanamori[16,19-20]使用台湾地震地区、南加州以及日本等三个地区的地震记录进行了研究。研究表明:τc方法的稳定性较高,能有效估算各地区的地震震级。国内的宋晋东和李山有[21]、金星等[22]、张红才等[23]也对τc方法进行了系列的研究,通过算例分析对比了τc方法与其它震级估算方法的性能。研究结果均表明:τc方法具备一定的优越性,比较适用于我国台网建设的现状[23]。
本文就上述τc方法进行了研究。针对地震波到时识别误差可能引起较大的τc计算误差的问题,提出了基于移动时窗的τc计算方法。使用广东省地震台网记录的测震数据对提出的方法进行了验证,同时,利用收集的测震记录建立了广东地区震级估算模型。
本文采用广东省地震台网记录的地震测震记录进行研究。所使用的数据包括随机选取的2013年至2018年广东省内共22个地震事件的垂直向速度数据,地震震级最小为ML 3.0级、最大为ML4.7级,数据采样频率为100 Hz。在研究过程中,选取每个地震事件中地震波形清晰的台站记录进行分析。因此,本文所使用记录数量合计为318条,详细的地震目录如表1所示。
基于Sato和Hirasawa[24]在1973年提出的震源动力模型,Kanamori[18]认为只要能获取地震位移数据前几秒的影响周期参数,即可根据该参数估计地震事件的震级。因此,在Nakamura提出的τpmax 方法的基础上,Kanamori提出了一种改进的地震卓越周期计算方法τc方法。τc的计算公式如下:
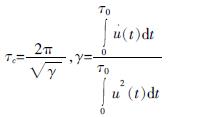 (1)
(1)
式(1)中,u(t)、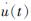 分别为位移和速度记录,积分区间[0,τ0]为从台站记录到地震信息开始至τ0 时刻的时间区间,即计算τc所使用的时间窗口长度为τ0 s。综合考虑震级估计的准确性及时效性,一般建议τ0取值为3 s。
分别为位移和速度记录,积分区间[0,τ0]为从台站记录到地震信息开始至τ0 时刻的时间区间,即计算τc所使用的时间窗口长度为τ0 s。综合考虑震级估计的准确性及时效性,一般建议τ0取值为3 s。
根据巴什瓦定律,式(1)可以写为,
 (2)
(2)
式(2)中,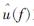 为位移u(t)的频谱,而〈f2〉为位移谱关于f2的平均频率。结合式(1)和(2)可知,τc值与地震位移谱重心位置处的周期相对应。因此,可利用τc参数来衡量地震规模。
为位移u(t)的频谱,而〈f2〉为位移谱关于f2的平均频率。结合式(1)和(2)可知,τc值与地震位移谱重心位置处的周期相对应。因此,可利用τc参数来衡量地震规模。
根据式(1)中τc的定义公式可知,积分区间[0,τ0]是影响τc计算值的关键因素。这涉及到两个重要参数:① 地震记录的初始时刻,这影响积分区间中0时刻的选择;② 计算时窗的长度,这决定了积分区间中τc的值。其中,根据国内外学者的研究经验,计算时窗的长度一般选取3 s为宜,地震记录的初始时刻目前一般由震相识别算法来确定。而通过震相识别获取的地震波到时会存在一定误差,这种误差可能会影响τc计算的稳定性。
式(2)指出,τc是可以反映地震动位移谱重心位置的周期的有效参数。而台站监测到的日常地脉动信号与地震发生时监测到的地震动信号在位移谱上是有明显差异的。因此,如果对监测数据进行连续的τc计算(如图1所示),在地震波到达台站的前后时刻,τc值应该会有显著变化。
基于移动时窗的计算方法,以0.1 s为移窗步长,3 s为计算窗口长度,对2017年02月28日广东东源3.0级地震中地震波形记录清晰的3个台站的数据进行计算,结果如图2所示。其中,LVY、DFH及GUL三个台站与震中的距离分别为21.87 km、32.23 km和38.37 km。图2显示,地震波到达各个台站时, τc值会急剧减小,随后逐渐恢复到震前水平。
此外,图3为图2的局部放大图,描述了各个台站接收到地震波前后的τc变化。对比各个台站的震中距,图3a指出,离震中最近的台站的τc值率先发生突变,而离震中最远的台站的τc值最后发生变化。这说明τc值的变化是由地震引起的,其变化时刻为地震波到达各个台站的时刻。其中,图3b以LVY台为例,描述了τc的突变过程。不难发现,τc值从日常水平的3.78减小到震时水平的0.16只耗时0.1 s。这说明,如果按照传统方法先进行地震波到时识别,再计算前3 s的τc值,0.1 s的到时识别误差可能导致近24倍的τc计算误差。因此,本文提出的移窗τc方法可通过τc的突变现象来更准确地、更稳定地确定地震前几秒的τc值,进而获取更稳定的震级估算结果。
为进一步研究移窗τc法的普适性,使用该方法对表1中的所有地震数据进行分析。分析过程中,先对各个记录的地震波到时时刻进行粗略估计,再截取到时时刻前后各10 s的数据,对合计共20 s的数据进行计算,结果如图4所示。显然,绝大部分记录的计算结果存在明显的τc值突变现象,只有极个别台站的τc值的变化比较缓慢,但也符合地震引起τc值减小的规律。同时,观察各个地震事件的计算结果还能发现,对于一次地震事件,所有台站的τc值几乎在同样的位置开始发生变化。这说明了τc发生突变的时刻便是地震波到达各个台站的时刻。而恰恰由于地震波到时识别的不准确,导致图4中各台站的τc变化位置不能完全重合。因此,图4 的计算结果表明:上述移窗τc计算方法具备很好的普适性,能通过各个台站的τc突变现象来确定P波前3 s的τc值。
图1 基于移动时窗的 τc计算方法
Fig.1 Proposed τc method based on moving window
图2 东源2017年3.0级地震τc计算结果
Fig.2 Value of τc of Dongyuan ML 3.0 earthquake in 2017
图3 东源2017年3.0级地震τc变化
Fig.3 Changes of τc in Dongyuan ML 3.0 earthquake in 2016
图4 基于移动时窗的 τc计算结果
Fig.4 Results of τc calculated by the proposed moving window method
基于上述移窗τc方法,对表1中地震事件进行计算,确定各个台站用于建立震级估算模型的P波前3 s的 τc值。其中,使用表1中震级不重复的编号为1、2、4、5、6、8、9、12、13、15和16的地震事件作为拟合样本,用于建立震级估算模型。使用剩余的地震事件作为测试样本,用于检验震级估算模型的泛化性。
图5为反映了拟合样本的τc值和震级关系及 τc的计算偏差。图中各个震级点上对应的τc误差是指该地震事件中所有台站记录计算得到的τc值方差。最后用于拟合震级估算模型的τc值为各地震事件中所有台站记录的τc值平均值。从图5可以看到,由上述移窗τc方法确定的P波前3 s的 τc值方差小,稳定性高。同时,图5显示由广东测震数据获取的τc值和震级之间存比较明显的线性关系,两者间的线性相关程度可用式(3)所示的相关系数进行衡量:
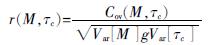 (3)
(3)
式(3)中,Cov(·)代表变量间的协方差,Var(·) 代表变量的方差。
将拟合样本数据代入式(3),计算得到由该样本得到的τc值与震级之间的相关系数为0.93,两者间存在非常强的线性关系。因此,可以使用式(4)中的线性模型进行建模:
M=aτc+b (4)
式(4)中,a和b为常数。
使用最小二乘法对模型进行拟合,拟合结果如图5虚线所示。可见,线性模型对样本数据的拟合效果很好,拟合残差为R=0.14。因此,根据拟合结果,可得到广东地区震级估算模型如式(5)所示:
M=4.09τc+2.22 (5)
使用测试样本对上述震级估算模型进行校验,结果如表2所示。可见,使用上述模型获取的估算震级与编目震级误差很小,最大偏差为0.5级,平均偏差只有0.11级。而在11个校验算例中,偏差大于0.2级的估算结果只有2个,其余估算结果的偏差均不大于0.1级。这说明,使用上述模型可较精确地使用测震数据估计广东地区的地震震级。
使用传统τc方法对地震震级进行估算时,需要先对地震波到时进行识别,再截取地震波的前3s数据计算τc。但地震波到时的识别误差可能引起较大的目标τc值计算误差。针对此问题,本文提出了基于移动时窗的τc方法。该方法对地震监测数据进行实时的τc计算,然后基于地震引起的 值突变现象来确定用于震级估计的τc值。使用该方法对广东省地区22个地震测震数据进行分析。结果表明,移窗τc方法可以稳定、准确地确定用于震级估算的目标τc值。同时,基于移窗τc方法,本文建立了广东地区的震级估算模型。模型检验结果指出,本文建立的震级估算模型可以准确地估计广东地区的地震震级,具备良好的泛化性。